��Ŀ����
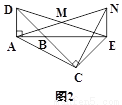
��ͼ����BAD�͡�BCE��Ϊ����ֱ�������Σ���BAD=��BCE=90�㣬MΪDE���е�.����E����ADƽ�е�ֱ�ߣ�������AM�ڵ�N.
(1)��A��B��C������ͬһ��ֱ����ʱ(��ͼ1)����֤��MΪAN�е�.
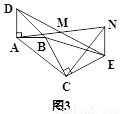
(2)��ͼ1�еġ�BCE�Ƶ�B��ת����A��B��E������ͬһ��ֱ����ʱ(��ͼ2)����֤����CANΪ����ֱ��������.
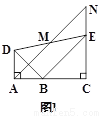
(3)��ͼ1�еġ�BCE�Ƶ�B��ת��ͼ3��λ��ʱ��(2)�еĽ����Ƿ���Ȼ����?����������֤����������������˵������.
��ϰ��ϵ�д�
 ͨ��ѧ��Ĭд����ϵ�д�
ͨ��ѧ��Ĭд����ϵ�д� ���ƽ̸�������ѡ����ĩ���100��ϵ�д�
���ƽ̸�������ѡ����ĩ���100��ϵ�д�
�����Ŀ


 x+3��AB��BC�ڵ�M��N������������
x+3��AB��BC�ڵ�M��N������������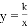 ��ͼ����M��N��
��ͼ����M��N��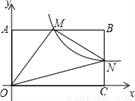
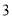 �ŷֱ��ʾ
�ŷֱ��ʾ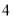 ��
��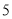 ��
��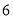 �ĺ����ƣ���֪С����ÿ��ȡһ����ȡ�Żصķ�ʽ���Ⱥ�ȡ��
�ĺ����ƣ���֪С����ÿ��ȡһ����ȡ�Żصķ�ʽ���Ⱥ�ȡ��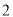 ���ƣ����һ����λ����ȡ����
���ƣ����һ����λ����ȡ����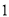 ���Ƶĺ���Ϊʮλ������
���Ƶĺ���Ϊʮλ������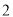 ���Ƶĺ���Ϊ��λ�������Ⱥ�ȡ��
���Ƶĺ���Ϊ��λ�������Ⱥ�ȡ��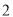 ������ɶ�λ����ÿһ�ֽ�������Ļ��ᶼ��ͬ�����б�����״��ʾ��ɶ�λ���Ŀ��������������ɵĶ�λ��Ϊ
������ɶ�λ����ÿһ�ֽ�������Ļ��ᶼ��ͬ�����б�����״��ʾ��ɶ�λ���Ŀ��������������ɵĶ�λ��Ϊ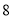 �ı����ĸ��ʣ�
�ı����ĸ��ʣ�