题目内容
12.已知等腰三角形的腰长为5,一腰上的高为4,则以底边为边长的正方形的面积为20或80.分析 根据题意作出图形分为高线在三角形内和高线在三角形外两种情况,然后根据勾股定理计算求解即可.
解答  解:由题意可作图.
解:由题意可作图.
如图1,AC=5,CD=4,CD⊥AB,
根据勾股定理可知:AD=3,
∴BD=2.
∴BC2=22+42=20.
如图2,AC=5,CD=4,CD⊥AB,
根据勾股定理可知:AD=3,
∴BD=8,
∴BC2=82+42=80.
故答案是:20或80.
点评 本题考查了勾股定理的运用以及等腰三角形的性质,正确作出图形利用三角形知识求解是解题关键.

练习册系列答案
相关题目
20.下列各数组中,不能作为直角三角形三边长的是( )
| A. | 9,12,15 | B. | 3,5,7 | C. | 7,24,25 | D. | 6,8,10 |
7.已知点(-2,y1),(3,y2)都在直线y=kx-1上,且k小于0,则y1与y2的大小关系是( )
| A. | y1<y2 | B. | y1=y2 | C. | y1>y2 | D. | 不能比较 |
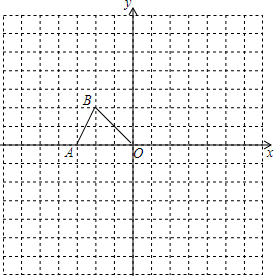 如图,在平面直角坐标系中,△AOB的位置如图所示,图中小正方形的边长均为1,请画出△AOB以点O为位似中心,放大到原来的2倍的位似图形,并写出放大后三角形三个顶点的坐标.
如图,在平面直角坐标系中,△AOB的位置如图所示,图中小正方形的边长均为1,请画出△AOB以点O为位似中心,放大到原来的2倍的位似图形,并写出放大后三角形三个顶点的坐标.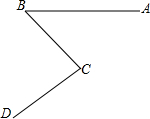 王林在《数学报》上看见一道作图题,请你帮他完成.
王林在《数学报》上看见一道作图题,请你帮他完成.