题目内容
1.已知抛物线y=$\frac{1}{2}$x2+bx与直线y=2x交于点O(0,0),A(a,12),点B是抛物线上O,A之间的一个动点,过点B分别作x轴、y轴的平行线与直线OA交于点C,E.(1)求抛物线的函数表达式;
(2)若点C为OA的中点,求EB的长.
分析 (1)将点A的坐标代入直线解析式求出a的值,继而将点A的坐标代入抛物线解析式可得出b的值,继而得出抛物线解析式;
(2)根据点B的横坐标为m,表示出点B的坐标是(m,$\frac{1}{2}$m2-m),点E的坐标为(m,2m),根据A,O点坐标得出C点坐标,进而得出m的值即可得出答案.
解答 解:(1)∵点A(a,12)在直线y=2x上,
∴12=2a,
解得:a=6,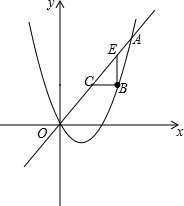
又∵点A是抛物线y=$\frac{1}{2}$x2+bx上的一点,
将点A(6,12)代入y=$\frac{1}{2}$x2+bx,可得b=-1,
∴抛物线解析式为y=$\frac{1}{2}$x2-x.
(2)如图所示:∵点B的横坐标为m,
∴点B的坐标是(m,$\frac{1}{2}$m2-m),点E的坐标为(m,2m),
∴BE=2m-($\frac{1}{2}$m2-m)=-$\frac{1}{2}$(m-3)2+$\frac{9}{2}$,
∵C为AO的中点,
∴C(3,6),
∴$\frac{1}{2}$m2-m=6,
解得:m1=1+$\sqrt{13}$,m2=1-$\sqrt{13}$(不合题意舍去),
∴BE=-$\frac{1}{2}$(m-3)2+$\frac{9}{2}$=-$\frac{1}{2}$(1+$\sqrt{13}$-3)2+$\frac{9}{2}$=2$\sqrt{13}$-4.
点评 此题考查了二次函数的性质、配方法、待定系数法求二次函数解析式的知识,表示出C、E、B点坐标是解题关键.

练习册系列答案
相关题目
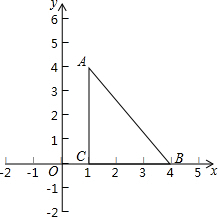 如图,在平面直角坐标系中,点A(1,4),点B(4,0),点C(1,0).
如图,在平面直角坐标系中,点A(1,4),点B(4,0),点C(1,0). 解一元一次方程的过程就是通过变形,把一元一次方程转化为x=a的形式.下面是解方程$\frac{2x-0.3}{0.5}-\frac{x+0.4}{0.3}=1$的主要过程,请在如图的矩形框中选择与方程变形对应的依据,并将它前面的序号填入相应的括号中.
解一元一次方程的过程就是通过变形,把一元一次方程转化为x=a的形式.下面是解方程$\frac{2x-0.3}{0.5}-\frac{x+0.4}{0.3}=1$的主要过程,请在如图的矩形框中选择与方程变形对应的依据,并将它前面的序号填入相应的括号中.
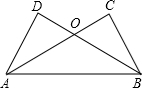 如图,已知∠C=∠D,∠ABC=∠BAD,AC与BD相交于点O,若AC=5,BO=3,则OD=2.
如图,已知∠C=∠D,∠ABC=∠BAD,AC与BD相交于点O,若AC=5,BO=3,则OD=2. 小张手机月基本费用为18元,某月,他把手机费中各项费用的情况制成扇形统计图(如图),则他该月的基本话费为90元.
小张手机月基本费用为18元,某月,他把手机费中各项费用的情况制成扇形统计图(如图),则他该月的基本话费为90元. 某产品每件成本28元,在试销阶段产品的日销售量y(件)与每件产品的日销售价x(元)之间的关系如图中的折线所示.为维持市场物价平衡,最高售价不得高出83元.
某产品每件成本28元,在试销阶段产品的日销售量y(件)与每件产品的日销售价x(元)之间的关系如图中的折线所示.为维持市场物价平衡,最高售价不得高出83元.