题目内容
【题目】在正方形![]() 中,连接
中,连接![]() ,
,![]() 为射线
为射线![]() 上的一个动点(与点
上的一个动点(与点![]() 不重合),连接
不重合),连接![]() ,
,![]() 的垂直平分线交线段
的垂直平分线交线段![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.
提出问题:当点![]() 运动时,
运动时,![]() 的度数是否发生改变?
的度数是否发生改变?
探究问题:
(1)首先考察点![]() 的两个特殊位置:
的两个特殊位置:
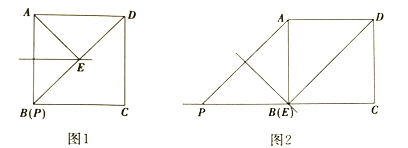
①当点![]() 与点
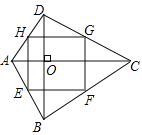
与点![]() 重合时,如图1所示,
重合时,如图1所示,![]() ____________
____________![]()
②当![]() 时,如图2所示,①中的结论是否发生变化?直接写出你的结论:__________;(填“变化”或“不变化”)
时,如图2所示,①中的结论是否发生变化?直接写出你的结论:__________;(填“变化”或“不变化”)
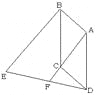
(2)然后考察点![]() 的一般位置:依题意补全图3,图4,通过观察、测量,发现:(1)中①的结论在一般情况下_________;(填“成立”或“不成立”)
的一般位置:依题意补全图3,图4,通过观察、测量,发现:(1)中①的结论在一般情况下_________;(填“成立”或“不成立”)
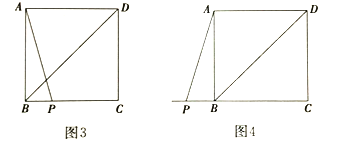
(3)证明猜想:若(1)中①的结论在一般情况下成立,请从图3和图4中任选一个进行证明;若不成立,请说明理由.
【答案】(1)①45;②不变化;(2)成立;(3)详见解析.
【解析】
(1)①②根据正方形的性质、线段的垂直平分线的性质即可判断;
(2)画出图形即可判断,结论仍然成立;
(3)如图2-1中或2-2中,作作EF⊥BC,EG⊥AB,证![]() 得∠AEG=∠PEF.由∠ABC=∠EFB=∠EGB=90°知∠GEF=∠GEP+∠PEF=90°.继而得∠AEP=∠AEG+∠GEP=∠PEF+∠GEP=90°.从而得出∠APE=∠EAP=45°.
得∠AEG=∠PEF.由∠ABC=∠EFB=∠EGB=90°知∠GEF=∠GEP+∠PEF=90°.继而得∠AEP=∠AEG+∠GEP=∠PEF+∠GEP=90°.从而得出∠APE=∠EAP=45°.
解(1)①当点P与点B重合时,如图1-1所示:

∵四边形ABCD是正方形,
∴∠APE=45°
②当BP=BC时,如图1-2所示,①中的结论不发生变化;
故答案为:45°,不变化.
(2) (2)如图2-1,如图2-2中,结论仍然成立;

故答案为:成立;
(3)证明一:如图所示.

过点![]() 作
作![]() 于点
于点![]() ,
,![]() 于点
于点![]() .
.
∵点![]() 在
在![]() 的垂直平分线上,
的垂直平分线上,
∴![]() .
.
∵四边形![]() 为正方形,
为正方形,
∴![]() 平分
平分![]() .
.
∴![]() .
.
∴![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
证明二:如图所示.

过点![]() 作
作![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
∵点![]() 在
在![]() 的垂直平分线上,
的垂直平分线上,
∴![]() .
.
∵四边形![]() 为正方形,
为正方形,
∴![]() ,
,
∴![]() .
.
∴![]() ,
,![]() .
.
∴![]() .
.
又∵![]() ,
,
∴![]() .
.
又∵![]() ,
,
∴![]() .
.
∴![]() .
.

【题目】将一些数排列成下表中的四列:
第1列 | 第2列 | 第3列 | 第4列 | |
第1行 | 1 | 4 | 5 | 10 |
第2行 | 4 | 8 | 10 | 12 |
第3行 | 9 | 12 | 15 | 14 |
… | … | … | … | … |
(1)第4行第1列的数是多少?直接写出答案;
(2)第17行的四个数之和是多少?请写出适当的过程;
(3)数100所在的行和列分别是多少?直接写出答案.
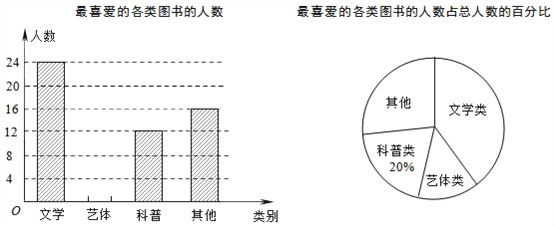
【题目】下表是某网约车公司的专车计价规则.
计费项目 | 起租价 | 里程费 | 时长费 | 远途费 |
单价 | 15元 | 2.5元/公里 | 1.5元/分 | 1元/公里 |
注:车费由起租价、里程费、时长费、远途费四部分构成,其中起租价15元含10分钟时长费和5公里里程费,远途费的收取方式为:行车里程10公里以内(含10公里)不收远途费,超过10公里的,超出部分每公里收1元.
(1)若小李乘坐专车,行车里程为20公里,行车时间为30分,则需付车费_______元.
(2)若小李乘坐专车,行车里程为![]() 公里,平均时速为
公里,平均时速为![]() ,则小李应付车费多少元? (用含
,则小李应付车费多少元? (用含![]() 的代数式表示)
的代数式表示)
(3)小李与小王各自乘坐专车,行车车费之和为76元,里程之和为15公里(其中小王的行车里程不超过5公里).如果行驶时间均为 20分钟,那么这两辆专车此次的行驶路程各为多少公里?