题目内容
【题目】我们给出如下定义：把对角线互相垂直的四边形叫做“对角线垂直四边形”.
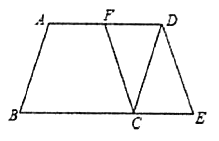
如图，在四边形
中，
，四边形就是“对角线垂直四边形”.
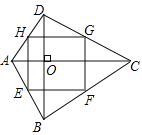
（1）下列四边形，一定是“对角线垂直四边形”的是_________.
①平行四边形 ②矩形 ③菱形 ④正方形
（2）如图，在“对角线垂直四边形”中，点
、
、
、
分别是边
、
、
、
的中点，求证：四边形
是矩形.
【答案】（1） ③④；（2）详见解析
【解析】
（1）根据“对角线垂直四边形"的定义求解；
（2）根据三角形中位线的性质得到HG//EF，HE//GF，则可判断四边形EFGH是平行四边形，再证明∠EHG=90°，然后判断四边形EFGH是矩形；
(1) 菱形和正方形是“对角线垂直四边形，故③④满足题意.
(2)证明：∵点
分别是边
、
、
、
的中点，
∴
，且
；
，且
；
.
∴
.
∴四边形
是平行四边形.
∵
，
∴
，
又∵，
∴
.
∴
.
∴
是矩形.
练习册系列答案
相关题目
