题目内容
已知xy≠1,5x2+2001x+9=0,9y2+2001y+5=0,求
.
| x |
| y |
考点:根与系数的关系
专题:计算题
分析:先把9y2+2001y+5=0变形得到5•(
)2+2001•
+9=0,加上5x2+2001x+9=0,于是可把x与
看作方程t2+2001t+9=0的两个根,然后根据根与系数的关系求解.
| 1 |
| y |
| 1 |
| y |
| 1 |
| y |
解答:解:∵9y2+2001y+5=0,
∴y≠0,
∴5•(
)2+2001•
+9=0,
而5x2+2001x+9=0,
∴x与
可看作方程t2+2001t+9=0的两个根,
∴x•
=9,
即
=9.
∴y≠0,
∴5•(
| 1 |
| y |
| 1 |
| y |
而5x2+2001x+9=0,
∴x与
| 1 |
| y |
∴x•
| 1 |
| y |
即
| x |
| y |
点评:本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-
,x1x2=
.
| b |
| a |
| c |
| a |

练习册系列答案
相关题目
下列算式运算结果最大的是( )
| A、-2+3 |
| B、-2×(-3) |
| C、-2-(-3) |
| D、-2÷(-3) |
下列由已知得出的结论,不正确的是( )
| A、已知m=n,则ma=na | ||||
| B、已知m=n,则m+a2=n+a2 | ||||
C、已知m=n,则
| ||||
| D、已知m=n,则m-a2=n-a2 |
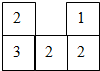 如图所示是一个由若干个相同的小立方块所搭成的几何体从上面看到的图形,小正方形中的数字表示在该位置上小立方块的个数,请画出它从正面和从左面看到的平面图形.
如图所示是一个由若干个相同的小立方块所搭成的几何体从上面看到的图形,小正方形中的数字表示在该位置上小立方块的个数,请画出它从正面和从左面看到的平面图形.