题目内容
已知⊙ 、⊙
、⊙ 外切于点
外切于点 ,经过点
,经过点 的任一直线分别与⊙
的任一直线分别与⊙ 、⊙
、⊙ 交于点
交于点 、
、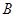 ,
,
(1)若⊙ 、⊙
、⊙ 是等圆(如图1),求证
是等圆(如图1),求证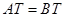 ;
;
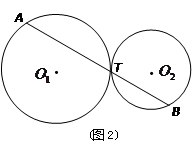
(2)若⊙ 、⊙
、⊙ 的半径分别为
的半径分别为 、
、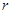 (如图2),试写出线段
(如图2),试写出线段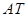 、
、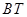 与
与 、
、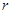 之间始终存在的数量关系(不需要证明).
之间始终存在的数量关系(不需要证明).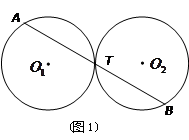
解:(1)联结
 .
.
∵⊙ .⊙
.⊙ 外切于点
外切于点 ,∴点T在
,∴点T在
 上.
上.
如图,过 .
. 分别作
分别作 .
. ,垂足为
,垂足为 、
、 ,
, 
∴  ∥
∥ .
.
∴  .
.
∵⊙ .⊙
.⊙ 是等圆,∴
是等圆,∴ .
.
∴ ,
,
∴ .
.
在⊙ 中,
中,
∵ ,
,
∴ .
.
同理  .
.
∴ ,即
,即 .
.
(2)线段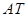 .
.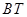 与
与 、
、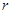 之间始终存在的数量关系是
之间始终存在的数量关系是
 .
.
解析

练习册系列答案
相关题目
已知⊙O与⊙O′外切于点C,它们的半径分别为R,r,AB为两圆外公切线,切点为A,B,则公切线的长AB等于( )
A、4
| ||
B、
| ||
C、2
| ||
| D、2Rr |
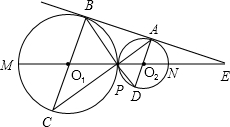 长线交⊙O1于C点,BP的延长线交⊙O2于D点,直线O1O2交⊙O1于M,交⊙O2于N,与BA的延长线交于点E.
长线交⊙O1于C点,BP的延长线交⊙O2于D点,直线O1O2交⊙O1于M,交⊙O2于N,与BA的延长线交于点E.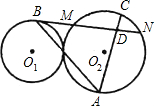 如图,已知⊙O1、⊙O2外切于点P,过P点的直线分别交⊙O1、⊙O2于B、A,⊙O1的切线BN交⊙O2于M、N,AC为⊙O2的弦,AC交MN于D,若AP=3,BP=2,则AD•AC=( )
如图,已知⊙O1、⊙O2外切于点P,过P点的直线分别交⊙O1、⊙O2于B、A,⊙O1的切线BN交⊙O2于M、N,AC为⊙O2的弦,AC交MN于D,若AP=3,BP=2,则AD•AC=( ) (1997•陕西)如图,已知⊙O1与⊙O2外切于点C,AB为两圆外公切线,切点为A,B,若⊙O1的半径为1,⊙O2的半径为3,则图中阴影部分的面积是( )
(1997•陕西)如图,已知⊙O1与⊙O2外切于点C,AB为两圆外公切线,切点为A,B,若⊙O1的半径为1,⊙O2的半径为3,则图中阴影部分的面积是( )