题目内容
（1998•大连）已知⊙O与⊙O′外切于点C，外公切线AB与连心线OO′交于点P，A、B为切点．AB=2
，大圆O的半径为3，则两条外公切线所夹的锐角的度数是（ ）
| 3 |
分析：根据切线的性质得出AE=BE=EC=
，再利用tan∠EO′B=
=
，得出∠EO′B=30°，进而求出∠P的度数，即可得出两条外公切线所夹的锐角的度数．
| 3 |
| BE |
| BO′ |
| ||
| 3 |
解答：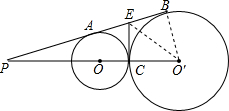
解：如图，作两圆的公切线EC，连接BO″，EO′，
∵⊙O与⊙O′外切于点C，外公切线AB与连心线OO′交于点P，A、B为切点，
∴O′B⊥PB，
∵EB，EC是⊙O′的切线，AE，EC是⊙O的切线，
∴EB=EC，AE=EC，
∴AE=BE=EC=
，
∵BO′=3，
∴在Rt△BEO′，
tan∠EO′B=
=
，
同理可得出：∠EO′C=30°，
∴∠P=30°，
∴两条外公切线所夹的锐角的度数是：60°．
故选：B．
解：如图，作两圆的公切线EC，连接BO″，EO′，∵⊙O与⊙O′外切于点C，外公切线AB与连心线OO′交于点P，A、B为切点，
∴O′B⊥PB，
∵EB，EC是⊙O′的切线，AE，EC是⊙O的切线，
∴EB=EC，AE=EC，
∴AE=BE=EC=
| 3 |
∵BO′=3，
∴在Rt△BEO′，
tan∠EO′B=
| BE |
| BO′ |
| ||
| 3 |
同理可得出：∠EO′C=30°，
∴∠P=30°，
∴两条外公切线所夹的锐角的度数是：60°．
故选：B．
点评：此题主要考查了切线长定理以及锐角三角函数的关系等知识，根据已知得出∠EO′C的度数是解题关键．
练习册系列答案
相关题目
（1998•大连）已知：二次函数y=-x2+2x+3
（1998•大连）已知：⊙O（如图）．求作：⊙O的内接正六边形ABCDEF（要求：只作图，不写作法，但须保留作图痕迹）