题目内容
如图,PA、PB分别切⊙O于A、B,连接PO、AB相交于D,C是⊙O上一点,∠C=60°。
(1)求∠APB的大小;
(2)若PO=20cm,求△AOB的面积。
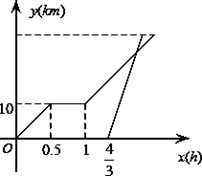
解:(1)∵PA、PB分别切⊙O于A、B,∴OA⊥PA,OB⊥PB。∴∠PAO=∠PBO=90°.1分
∵∠C=60°,∴∠AOB=2∠C=2×60°=120°
∴∠APB=360°-∠PAO-∠PBO-∠AOB= 60°。
60°。
∵PA、PB分别切⊙O于A、B,∴∠A PO=
PO= ∠APB=
∠APB= ×60°=30°,PA=PB。
×60°=30°,PA=PB。
∴P在AB的垂直平分线上。
∵OA=OB,∴O在AB的垂直平分线上,即OP是AB的垂直平分线,
∴OD⊥AB,AD=BD= AB。∵∠PAO=90°,∴∠AOP=60°。
AB。∵∠PAO=90°,∴∠AOP=60°。
在Rt△PAO中,AO= PO=
PO= ×20=10,
×20=10,
在Rt△AOD中,AD=AO•sin60°=10×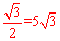 ,OD=OA•cos60°=10×
,OD=OA•cos60°=10× =5,
=5,
∴AB=2AD=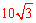 ,
,
∴△AOB的面积为: AB•OD=
AB•OD=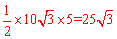 (cm2)。
(cm2)。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
计算sin245°+cos30°•tan60°,其结果是( )
|
| A. | 2 | B. | 1 | C. |
| D. |
|


 -
-  = 2.
= 2. 庆交通的发展,搭乘公交车从家去参观东水门长江大桥,预计1个小时能到达.行驶了半个小时,刚好行驶了一半路程,遇到堵车道路被“堵死”,堵了几分钟突然发现旁边刚好有一个轻轨站,于是王大爷转乘轻轨去观看大桥(轻轨速度大于公交车速度),结果按预计时间到达.下面能反映王大爷距大桥的距离
庆交通的发展,搭乘公交车从家去参观东水门长江大桥,预计1个小时能到达.行驶了半个小时,刚好行驶了一半路程,遇到堵车道路被“堵死”,堵了几分钟突然发现旁边刚好有一个轻轨站,于是王大爷转乘轻轨去观看大桥(轻轨速度大于公交车速度),结果按预计时间到达.下面能反映王大爷距大桥的距离 (千米)与时间
(千米)与时间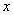 (小时)的函数关系的大致图象是( )
(小时)的函数关系的大致图象是( )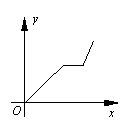
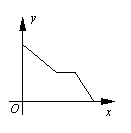

 x轴上,∠ABC=90°,AB=BC,OA=1,OB=4,抛物
x轴上,∠ABC=90°,AB=BC,OA=1,OB=4,抛物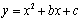 经过A、C两点.
经过A、C两点.

 ,
, ,
, ,
, 中为无理数的是( ).
中为无理数的是( ).