Question

如图，在平面直角坐标系中，△ABC的边AB在x轴上，∠ABC=90°，AB=BC，OA=1，OB=4，抛物

线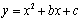经过A、C两点．

（1）求抛物线的解析式及其顶点坐标；

（2）如图①，点P是抛物线上位于x轴下方的一点，点Q与点P关于抛物线的对称轴对称，过点P、Q分别向x轴作垂线，垂足为点D、E，记矩形DPQE的周长为d，求d的最大值，并求出使d最大值时点P的坐标；

 （3）如图②，点M是抛物线上位于直线AC下方的一点，过点M作MF⊥AC于点F，连接MC，作MN∥BC交直线AC于点N，若MN将△MFC的面积分成2：3两部分，请确定M点的坐标．

 

Answer 1

 解：（1）由已知得：A（-1，0）、C（4，5）          ………1分

∵二次函数的图像经过点A（-1，0）C(4,5)

∴      解得              ………2分

    ∴抛物线解析式为                   ………3分

    ∵   

∴顶点坐标为（1，-4）                          ………4分

 （2）由（1）知抛物线的对称轴为直线x=1

     设点P为（（t，），

∵P、Q为抛物线上的对称点

     ∴