题目内容
15．
如图，在单位长度为1的方格纸中．△ABC如图所示：（1）请在方格纸上建立平面直角坐标系，使A（0，0），C（4，-4）并求出B点坐标（-2，-4）；
（2）以点A为位似中心，位似比为1：2，在第一，二象限内将△ABC缩小，画出缩小后的位似图形△A'B'C'；
（3）计算△A'B'C'的面积S．
分析 （1）直接利用A，C点坐标建立平面直角坐标系，进而得出B点坐标；
（2）利用位似图形的性质分别得出对应点位置进而得出答案；
（3）直接利用三角形面积求法得出其面积．
解答 解：
（1）如图所示：建立正确坐标系，B（-2，-4）；
故答案为：（-2，-4）；
（2）如图所示：△A'B'C'即为所求；
（3）△A'B'C'的面积S=$\frac{1}{2}$×2×3=3．
点评 此题主要考查了位似变换，正确建立平面直角坐标系是解题关键．
练习册系列答案
相关题目
如图，在四边形ABCD中，∠ABC=30°，∠ADC=60°，AD=DC，若AB=5，BC=6，求BD的长．（提示：把△DCB绕点C顺时针旋转60°到ACB′，连BB′）
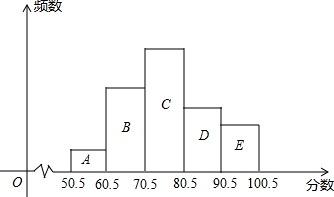从某校参加科普知识竞赛的学生试卷中，抽取一个样本了解竞赛成绩的分布情况，将样本分成A、B、C、D、E五个组，绘制成如图所示的频数分布直方图，图中A、B、C、D、E各小组的长方形的高的比是l：4：6：3：2，且A组的频数是5，请结合直方图提供的信息，解答下列问题．