Question

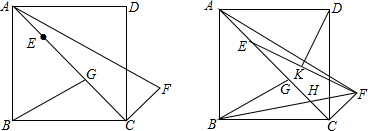
1．已知如图，正方形ABCD，AC为对角线，CF⊥AC，连接AF，点E在AC上，AE=CF，点G为线段CE中点，连接BG，
（1）求证：∠AFC=∠AGB；
（2）连接BF交线段AC于点H，连接EF，DK⊥EF，垂足为点K，若BH=2FH，请你探究线段HG和DK之间的数量关系，并证明你的结论．

Answer 1

分析 （1）连接BD，利用两边对应成比例且夹角相等证明△ACF∽△BOG，得∠AFC=∠AGB；
（2）连接对角线BD，得直角△EOM和直角△BOG，设OG=x，利用平行成比例性质表示出边FC、BO、GH、OM、DM的长，再利用三角函数表示出DK的长，最后计算$\frac{DK}{GH}$的值，得出结论．

解答 证明：（1）如图1，连接BD交AC于点O，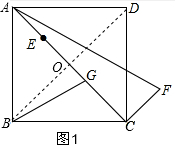
∵四边形ABCD是正方形，
∴AO=BO=CO=$\frac{1}{2}$AC，∠BOC=90°，$\frac{AC}{OB}=\frac{2}{1}$，
∵∠ACF=90°，
∴∠BOC=∠ACF，
∵EG=CG，
∴AO-EG=CO-CG=OG，
∵AO-EG=AE+EO-（OE+OG）=AE-OG，
∴AE-OG=OG，
∴AE=2OG，
∴CF=AE=2OG，
∴$\frac{CF}{OG}=\frac{2}{1}$，
∴$\frac{AC}{OB}=\frac{CF}{OG}$，
∴△ACF∽△BOG，
∴∠AFC=∠AGB；
（2）如图2，DK=$\frac{3\sqrt{10}}{5}$GH，理由是：
连接BD交AC于O，交EF于M，
设OG=x，则FC=2x，
∵OB∥FC，
∴$\frac{BH}{HF}=\frac{OB}{FC}=\frac{OH}{HC}=\frac{2}{1}$，
∴OB=2FC=4x，OH=2HC，
则GH=OH-OG=$\frac{8x}{3}$-x=$\frac{5x}{3}$，OE=OA-AE=4x-2x=2x，
∵OM∥FC，
∴$\frac{OM}{FC}=\frac{OE}{EC}$，
∴$\frac{OM}{2x}=\frac{2x}{2x+4x}$，
∴OM=$\frac{2X}{3}$，
由勾股定理得：EM=$\sqrt{（2x）^{2}+（\frac{2x}{3}）^{2}}$=$\frac{2\sqrt{10}x}{3}$，
则DM=4x-$\frac{2x}{3}$=$\frac{10x}{3}$，
在△EOM和△DKM中，∠EOM=∠MKD，∠EMO=∠KMD，
∴∠CEF=∠MDK，
∵cos∠CEF=$\frac{OE}{EM}$，cos∠MDK=$\frac{DK}{DM}$，
∴$\frac{OE}{EM}=\frac{DK}{DM}$，
∴$\frac{2x}{\frac{2\sqrt{10}x}{3}}$=$\frac{DK}{\frac{10x}{3}}$，
∴DK=$\sqrt{10}x$，
∴$\frac{DK}{GH}$=$\frac{\sqrt{10}x}{\frac{5x}{3}}$=$\frac{3\sqrt{10}}{5}$，
则DK=$\frac{3\sqrt{10}}{5}$GH．

点评 本题是四边形的综合题，考查了正方形和平行线截线段成比例的性质，在几何证明中，如果不能求边的具体长度，可以设某一小边为x，利用比例式表示一些线段的长，最后得出结论；同时可以利用同角的三角函数值来求边的长度，比利用勾股定理要简单．