题目内容
18.已知a=$\sqrt{3}$$+\sqrt{2}$,b=$\sqrt{3}$$-\sqrt{2}$,则a2b-ab2=2$\sqrt{2}$.分析 由题意可知:ab=1,a-b=2$\sqrt{2}$,由此把代数式因式分解,进一步代入求得答案即可.
解答 解:∵a=$\sqrt{3}$$+\sqrt{2}$,b=$\sqrt{3}$$-\sqrt{2}$,
∴ab=1,a-b=2$\sqrt{2}$,
∴a2b-ab2
=ab(a-b)
=2$\sqrt{2}$.
故答案为:2$\sqrt{2}$.
点评 此题考查二次根式的化简求值,注意代数式的特点,先分解因式再代入求得数值即可.

练习册系列答案
相关题目
13.下列式子中,属于最简二次根式的是( )
| A. | $\sqrt{7}$ | B. | $\sqrt{9}$ | C. | $\sqrt{20}$ | D. | $\sqrt{\frac{1}{3}}$ |
3.已知:点P的坐标为(-2,1),则点P所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
7.以下四点:(1,2),(2,3),(0,1),(-2,3)在直线y=2x+1上的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
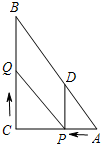 如图,在Rt△ABC中,∠C=90°,AC=9,BC=12,动点P从点A开始,沿边AC向点C以每秒1个单位长度的速度运动,动点Q从点C开始,沿边CB向点B以每秒2个单位长度的速度运动,过点P作PD∥BC,交AB于点D,连结PQ.点P,Q分别从点A,C同时出发,当其中一点到达端点时,另两个点也随之停止运动,设运动时间为t秒(t≥0).
如图,在Rt△ABC中,∠C=90°,AC=9,BC=12,动点P从点A开始,沿边AC向点C以每秒1个单位长度的速度运动,动点Q从点C开始,沿边CB向点B以每秒2个单位长度的速度运动,过点P作PD∥BC,交AB于点D,连结PQ.点P,Q分别从点A,C同时出发,当其中一点到达端点时,另两个点也随之停止运动,设运动时间为t秒(t≥0). 按下列要求画图,并解答问题:
按下列要求画图,并解答问题: 甲、乙两人沿相同的路线由A地到B地匀速前进,A、B两地间的路程为20km,他们前进的路程为s(km),甲出发后的时间为t(h),甲、乙前进的路程与时间的函数图象如图所示,根据图象信息,下列说法正确个数为( )
甲、乙两人沿相同的路线由A地到B地匀速前进,A、B两地间的路程为20km,他们前进的路程为s(km),甲出发后的时间为t(h),甲、乙前进的路程与时间的函数图象如图所示,根据图象信息,下列说法正确个数为( )