题目内容
阅读理【解析】
在平面直角坐标系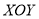 中,对于任意两点
中,对于任意两点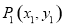 与
与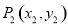 的“非常距离”给出下列定义: 若
的“非常距离”给出下列定义: 若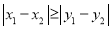 ,则点
,则点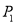 与
与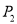 的“非常距离”为
的“非常距离”为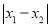 ;
;
若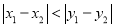 ,则点
,则点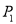 与
与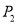 的“非常距离”为
的“非常距离”为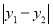 . 例如:点
. 例如:点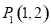 ,点
,点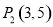 ,因为
,因为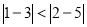 ,所以点
,所以点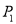 与
与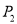 的“非常距离”为
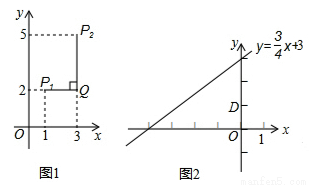
的“非常距离”为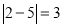 ,也就是图1中线段
,也就是图1中线段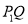 与线段
与线段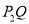 长度的较大值(点Q为垂直于
长度的较大值(点Q为垂直于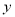 轴的直线
轴的直线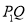 与垂直于
与垂直于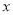 轴的直线
轴的直线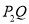 的交点).
的交点).
(1)已知点A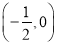 ,B为
,B为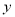 轴上一个动点.
轴上一个动点.
①若点B(0,3),则点A与点B的“非常距离”为 ;
②若点A与点B的“非常距离”为2,则点B的坐标为 ;
③直接写出点A与点B的“非常距离”的最小值 .
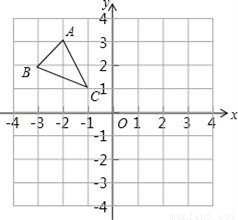
(2)已知点D(0,1),点C是直线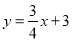 上的一个动点,如图2,求点C与点D“非常距离”的最小值及相应的点C的坐标.
上的一个动点,如图2,求点C与点D“非常距离”的最小值及相应的点C的坐标.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
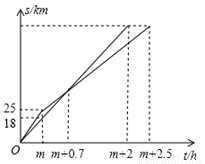
某日孙老师佩戴运动手环进行快走锻炼,两次锻炼后数据如下表.与第一次锻炼相比,孙老师第二次锻炼步数增长的百分率是其平均步长减少的百分率的3倍.根据经验已知孙老师第二次锻炼时平均步长减少的百分率小于0.5.
项目 | 第一次锻炼 | 第二次锻炼 | ||
步数(步) | 10000 | ① | ||
平均步长(米/步) | 0.6 | ② | ||
距离(米) | 6000 | 7020 |
注:步数×平均步长=距离.
(1)求孙老师第二次锻炼时平均步长减少的百分率;
(2)孙老师发现好友中步数排名第一为24000步,因此在两次锻炼结束后又走了500米,使得总步数恰好为24000步,求孙老师这500米的平均步长.


 C. y=
C. y= D. y=
D. y=
 轴距离是__________,到
轴距离是__________,到 轴距离是_____________.
轴距离是_____________.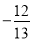 ,-20,+9.78,+68,0.45,+
,-20,+9.78,+68,0.45,+ .
.