题目内容
如图,PA、PB是⊙O的切线,A、B为切点,∠OAB=30°,OA=3,则阴影部分面积为 .
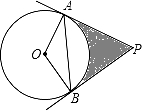
9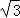 ﹣3π【考点】切线的性质;扇形面积的计算.
﹣3π【考点】切线的性质;扇形面积的计算.
【分析】根据四边形的内角和为360°,根据切线的性质可知:∠OAP=∠OBP=90°,求出∠AOB的度数,进一步求得∠APB的度数,然后根据阴影部分的面积等于四边形OAPB的面积减去扇形AOB的面积即可求得.
【解答】解:∵在△ABO中,OA=OB,∠OAB=30°,
∴∠AOB=180°﹣2×30°=120°,
∵PA、PB是⊙O的切线,
∴OA⊥PA,OB⊥PB,即∠OAP=∠OBP=90°,
∴在四边形OAPB中,∠APB=360°﹣120°﹣90°﹣90°=60°.
连接OP.
根据切线长定理得∠APO=30°,
∴OP=2OA=6,AP=OP•cos30°=3 ,∠AOP=60°.
,∠AOP=60°.
∴四边形的面积=2S△AOP=2×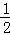 ×3×3
×3×3 =9
=9 ;扇形的面积是
;扇形的面积是 =3π,
=3π,
∴阴影部分的面积是9 ﹣3π.
﹣3π.
故答案为9 ﹣3π.
﹣3π.

【点评】本题考查了切线长定理、切线的性质定理以及30°的直角三角形的性质.关键是熟练运用扇形的面积计算公式,能够把四边形的面积转化为三角形的面积计算..

练习册系列答案
相关题目

 =
=
 ﹣1.
﹣1. 对应的图象为( )
对应的图象为( ) B.
B. C.
C. D.
D.
 ,2) D.与x轴无交点
,2) D.与x轴无交点
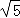 C.2 D.1
C.2 D.1

 B.
B.
 C.
C.
 D.
D.
 =1,则x
=1,则x +
+ 的值是
的值是