题目内容
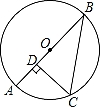
如图,⊙O半径为2,AB为⊙O的直径,BC为⊙O的一条弦,若∠ABC=30°,过点C作AB的垂线,垂足为点D,则CD长为( )
A.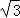 B.
B.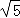 C.2 D.1
C.2 D.1
A【考点】圆周角定理;含30度角的直角三角形;勾股定理.
【分析】 连接OC,根据圆周角定理可得出∠AOC的度数,再由锐角三角函数的定义即可得出结论.
连接OC,根据圆周角定理可得出∠AOC的度数,再由锐角三角函数的定义即可得出结论.
【解答】解:连接OC,
∵∠ABC=30°,
∴∠AOC=60°.
∵CD⊥AB,∠AOC=60°,OC=2,
∴CD=OC•sin60°=2× =
=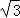 .
.
故选A.

【点评】本题考查的是圆周角定理,熟知在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半是解答此题的关键.

练习册系列答案
相关题目




 的值为0,则x=
的值为0,则x= 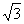 B
B .
.  C.
C.  D.
D. 