题目内容
19. 小亮和爸爸上山游玩,小亮乘坐缆车,爸爸步行,两人相约在山顶的缆车终点会合.已知爸爸行走到缆车终点的路程是缆车到山顶的线路长的2倍,小亮在爸爸出发后50分钟才乘上缆车,缆车的平均速度为180米/分钟.设爸爸出发x 分钟后行走的路程为y米.图中的折线表示爸爸在整个行走过程中y随x的变化关系.
小亮和爸爸上山游玩,小亮乘坐缆车,爸爸步行,两人相约在山顶的缆车终点会合.已知爸爸行走到缆车终点的路程是缆车到山顶的线路长的2倍,小亮在爸爸出发后50分钟才乘上缆车,缆车的平均速度为180米/分钟.设爸爸出发x 分钟后行走的路程为y米.图中的折线表示爸爸在整个行走过程中y随x的变化关系.(1)爸爸行走的总路程是3600米,他途中休息了20分钟.
(2)分别求出爸爸在休息前和休息后所走的路程段上的步行速度.
(3)当小亮到达缆车终点时,爸爸离缆车终点的路程是多少?
分析 根据图象获取信息:
(1)爸爸到达山顶用时80分钟,中途休息了20分钟,行程为3600米;
(2)休息前30分钟行走1950米,休息后20分钟行走(3600-1950)米.
(3)求小亮到达缆车终点的时间,计算爸爸行走路程,求离缆车终点的路程.
解答 解:(1)根据图象知:爸爸行走的总路程是3600米,他途中休息了20分钟.
故答案为 3600,20;
(2)爸爸休息前的速度为:$\frac{1950}{30}=65$(米/分),
爸爸休息后的速度为:$\frac{3600-1950}{80-50}=55$(米/分);
(3)小亮所用时间:$\frac{3600}{\frac{2}{180}}=10$(分),
爸爸比小亮迟到80-50-10=20(分),
则小亮到达终点时,爸爸离缆车终点的路程为:20×55=1100(米).
点评 此题考查一次函数及其图象的应用,从图象中获取相关信息是关键.此题第3问难度较大.

练习册系列答案
相关题目
7.李师傅做了一个三角形的工件,其中两条边长分别为30cm和80cm,则另一边长度可能是( )
| A. | 30cm | B. | 50cm | C. | 60cm | D. | 120cm |
4.已知△ABC的三个内角∠A、∠B、∠C满足关系式∠B+∠C=3∠A,则此三角形( )
| A. | 一定有一个内角为60° | B. | 一定有一个内角为45° | ||
| C. | 一定是直角三角形 | D. | 一定是钝角三角形 |
11.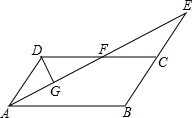 如图,在平行四边形ABCD中,AB=4,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为DC的中点,DG⊥AE,垂足为G.若AE=4$\sqrt{3}$,则DG的长为( )
如图,在平行四边形ABCD中,AB=4,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为DC的中点,DG⊥AE,垂足为G.若AE=4$\sqrt{3}$,则DG的长为( )
 如图,在平行四边形ABCD中,AB=4,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为DC的中点,DG⊥AE,垂足为G.若AE=4$\sqrt{3}$,则DG的长为( )
如图,在平行四边形ABCD中,AB=4,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为DC的中点,DG⊥AE,垂足为G.若AE=4$\sqrt{3}$,则DG的长为( )| A. | $\sqrt{7}$ | B. | $\sqrt{5}$ | C. | 1 | D. | $\sqrt{2}$ |
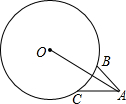 如图,△ABC中,BC=4,∠BAC=45°,以$4\sqrt{2}$为半径,过B、C两点作⊙O,连OA,则线段OA的最大值为2$\sqrt{2}$+2+2$\sqrt{7}$.
如图,△ABC中,BC=4,∠BAC=45°,以$4\sqrt{2}$为半径,过B、C两点作⊙O,连OA,则线段OA的最大值为2$\sqrt{2}$+2+2$\sqrt{7}$.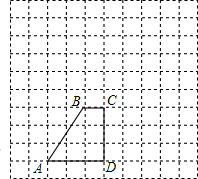 (1)如图在10×10的方格纸中,梯形ABCD是直角梯形,请在图中以CD为对称轴画一个关于直线CD对称的直角梯形EFCD,使它与梯形ABCD构成一个等腰梯形AEFB.(不要求写作法)
(1)如图在10×10的方格纸中,梯形ABCD是直角梯形,请在图中以CD为对称轴画一个关于直线CD对称的直角梯形EFCD,使它与梯形ABCD构成一个等腰梯形AEFB.(不要求写作法)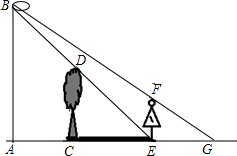 如图,小彬和小颖放学回家时发现路边一棵小树在路灯下的影子很清晰,他们想利用所学知识,测量一下小树的高度,于是通过步测,测得小树CD底部离路灯杆AB底部8米,树影CE长8米,小颖身高1.6米,她走到树影顶端E处,让小彬测得她在同一路灯下的影子EG长为4米.
如图,小彬和小颖放学回家时发现路边一棵小树在路灯下的影子很清晰,他们想利用所学知识,测量一下小树的高度,于是通过步测,测得小树CD底部离路灯杆AB底部8米,树影CE长8米,小颖身高1.6米,她走到树影顶端E处,让小彬测得她在同一路灯下的影子EG长为4米.