题目内容

如图，在△ABC中，点D、E分别在AB、AC上，DE∥BC．若AD=4，DB=2，则
DE
BC
的值为（　　）
A、
1
2
B、
2
3
C、
3
4
D、2
考点：相似三角形的判定与性质
专题：
分析：首先根据DE∥BC，得出△ADE∽△ABC，即可得出
AD
AB
=
DE
BC
，进而得出
DE
BC
的值．
解答：解：∵DE∥BC，
∴△ADE∽△ABC，
∴
AD
AB
=
DE
BC
，
∵AD=4，DB=2，
∴
AD
AB
=
DE
BC
=
4
4+2
=
2
3
．
则
DE
BC
的值为
2
3
．
故选：B．
点评：此题主要考查了相似三角形的判定与性质，根据已知得出△ADE∽△ABC是解题关键．
练习册系列答案
相关题目
已知△ABC中，AB=4
2
，AC=5，BC=7．求∠B的度数．
计算：（-1）2013•|-1|+2cos30°+（
2
-2）0-
27
+（-
1
2
）-1．
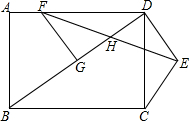如图，点E为矩形ABCD外一点，DE⊥BD于点D，DE=CE，BD的垂直平分线交AD于点F，交BD于点G．连接EF交BD于点H．
（1）若∠CDE=∠DEH=
1
2
∠HEC，求∠ABG的度数；
（2）求证：H是EF的中点．
甲、乙两名学生在某次打靶游戏中各射击4次，两人的测试成绩如下（单位：环）：
甲  6     7   8    9
乙  6.5   6.5  8.5  8.5
则测试成绩比较稳定的是
 
（填“甲”或“乙”）．
已知y=y1+y2，其中y1与x成反比例，y2与（x-2）成正比例，当x=1时，y=-1；x=3时，y=3．
（1）求y与x的函数关系；       
（2）当x=1时，y的值．
在比例尺为1：9000的重庆地图上，测得A、B两地的距离为16cm，则AB两地的实际距离为
 
米．
不等式组
x-1＞0
x＜2
的解集在数轴上表示正确的是（　　）
A、
B、
C、
D、
如图，在?ABCD中，点E为AD的中点，连接BE，交AC于点F，则
S△AEF
S△ABF
=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网