题目内容
 如图,在?ABCD中,点E为AD的中点,连接BE,交AC于点F,则
如图,在?ABCD中,点E为AD的中点,连接BE,交AC于点F,则| S△AEF |
| S△ABF |
考点:相似三角形的判定与性质,平行四边形的性质
专题:探究型
分析:设?ABCD的面积为s,S△ABF=a,即S△AEF+a=
,根据平行四边形的性质可知S△ABC=
S?ABCD=
,即S△BCF+a=
,再由相似三角形的判定定理可得出△AEF∽△BCF,故可得出S△AEF:S△BCF=1:4,由此可用s表示出a的值,进而得出结论.
| s |
| 4 |
| 1 |
| 2 |
| s |
| 2 |
| s |
| 2 |
解答:解:?ABCD的面积为s,S△ABF=a,即S△AEF+a=
,
∵四边形ABCD是平行四边形,
∴S△ABC=
S?ABCD=
,即S△BCF+a=
,
∵四边形ABCD是平行四边,
∴AD=BC,
∵点E为AD的中点,
∴AE=DE,
∴AE:BC=AE:AD=1:2,
∵AD∥BC,
∴△AEF∽△BCF,
∴S△AEF:S△BCF=AE2:BC2=1:4,
∴
=
,解得a=
,即S△ABF=
,
∴S△AEF=
-a=
-
=
,
∴
=
=
.
故答案为:
.
| s |
| 4 |
∵四边形ABCD是平行四边形,
∴S△ABC=
| 1 |
| 2 |
| s |
| 2 |
| s |
| 2 |
∵四边形ABCD是平行四边,
∴AD=BC,
∵点E为AD的中点,
∴AE=DE,
∴AE:BC=AE:AD=1:2,
∵AD∥BC,
∴△AEF∽△BCF,
∴S△AEF:S△BCF=AE2:BC2=1:4,
∴
| ||
|
| 1 |
| 4 |
| s |
| 6 |
| s |
| 6 |
∴S△AEF=
| s |
| 4 |
| s |
| 4 |
| s |
| 6 |
| s |
| 12 |
∴
| SAEF |
| S△ABF |
| ||
|
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查的是相似三角形的判定与性质,熟知相似三角形的判定与性质及平行四边形的性质是解答此题的关键.

练习册系列答案
 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
 如图,在△ABC中,点D、E分别在AB、AC上,DE∥BC.若AD=4,DB=2,则
如图,在△ABC中,点D、E分别在AB、AC上,DE∥BC.若AD=4,DB=2,则| DE |
| BC |
A、
| ||
B、
| ||
C、
| ||
| D、2 |
在2,O,-
,-1四个数中最小是( )
| 1 |
| 2 |
| A、0 | ||
B、
| ||
| C、-1 | ||
| D、2 |
 如图,△ACF内接于⊙O,AB是⊙O直径,弦CD⊥AB于E,若CD=BE=8,则sin∠AFC的值为( )
如图,△ACF内接于⊙O,AB是⊙O直径,弦CD⊥AB于E,若CD=BE=8,则sin∠AFC的值为( )A、
| ||||
B、
| ||||
C、
| ||||
| D、以上都不对 |
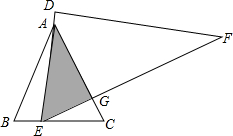 如图,等边△ABC中,AB=6,将一直角三角板DEF的60°角的顶点E置于边BC上移动(不与B、C重合),移动过程中,始终满足直角边DE经过点A,斜边EF交AC于点G.
如图,等边△ABC中,AB=6,将一直角三角板DEF的60°角的顶点E置于边BC上移动(不与B、C重合),移动过程中,始终满足直角边DE经过点A,斜边EF交AC于点G.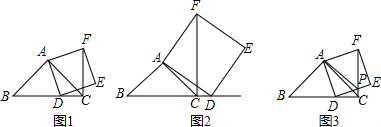
 一艘轮船沿长江顺流从武汉开往上海,行驶6小时后,发现船上一救生艇掉入江中,然后立即返回,再行驶3小时碰见救生艇.下图是轮船离出发地的距离与时间的函数关系,已知水流速度为5千米/时,则救生艇在轮船出发
一艘轮船沿长江顺流从武汉开往上海,行驶6小时后,发现船上一救生艇掉入江中,然后立即返回,再行驶3小时碰见救生艇.下图是轮船离出发地的距离与时间的函数关系,已知水流速度为5千米/时,则救生艇在轮船出发 如图为杨辉三角系数表,它有许多规律,如指导读者按规律写出如(a+b)n(其中n为正整数)展开式的系数,请你仔细观察下表中的规律,填出(a+b)4展开式中所缺的项.
如图为杨辉三角系数表,它有许多规律,如指导读者按规律写出如(a+b)n(其中n为正整数)展开式的系数,请你仔细观察下表中的规律,填出(a+b)4展开式中所缺的项. 据新华网2月28日公布,全国5个民族自治区参加第十二届全国人大代表会议的人数的平均数是49.8人,新疆地区60人,其余数据制成如图所示的不完整的条形统计图.
据新华网2月28日公布,全国5个民族自治区参加第十二届全国人大代表会议的人数的平均数是49.8人,新疆地区60人,其余数据制成如图所示的不完整的条形统计图.