题目内容
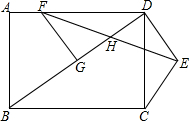 如图,点E为矩形ABCD外一点,DE⊥BD于点D,DE=CE,BD的垂直平分线交AD于点F,交BD于点G.连接EF交BD于点H.
如图,点E为矩形ABCD外一点,DE⊥BD于点D,DE=CE,BD的垂直平分线交AD于点F,交BD于点G.连接EF交BD于点H.(1)若∠CDE=∠DEH=
| 1 |
| 2 |
(2)求证:H是EF的中点.
考点:矩形的性质,全等三角形的判定与性质
专题:压轴题
分析:(1)设∠CDE=x°,则∠CDE=∠DCE=x°,∠DEH=x°,∠HEC=2x°,根据∠CDE+∠DEC+∠DCE=180°得出5x=180°,求出x即可;
(2)连接AC,GE,求出GD=GC,得出在CD的垂直平分线上,E在CD的垂直平分线上,推出GE为CD的垂直平分线,求出DM=CM,求出FD∥GE,FG∥DE,求出四边形FDEG是平行四边形,根据平行四边形性质推出即可.
(2)连接AC,GE,求出GD=GC,得出在CD的垂直平分线上,E在CD的垂直平分线上,推出GE为CD的垂直平分线,求出DM=CM,求出FD∥GE,FG∥DE,求出四边形FDEG是平行四边形,根据平行四边形性质推出即可.
解答:(1)解:设∠CDE=x°,
∵DE=CE,
∴∠CDE=∠DCE=x°,
∵∠CDE=∠DEH=
∠HEC,
∴∠deh=x°,∠HEC=2x°,
∵∠CDE+∠DEC+∠DCE=180°,
∴5x=180°,
x=36°,
∵DE⊥BD,
∴∠EDB=90°,
∴∠BDC=90°-36°=54°,
∵四边形ABCD是矩形,
∴AB∥CD,
∴∠ABG=∠BDC=54°;
(2)证明:
连接AC,GE,
∵四边形ABCD是矩形,
∴AC=BD,AG=GC,BG=GD,
∴GD=GC,
∴G在CD的垂直平分线上,
∵DE=CE,
∴E在CD的垂直平分线上,
∴GE为CD的垂直平分线,
∴DM=CM,
∵BG=DG,
∴GM∥BC,
∴∠DGE=∠DBC,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DBC=∠FDG,
∴∠DGE=∠FDG,
∴FD∥GE,
∵FG⊥BD,DE⊥BD,
∴FG∥DE,
∴四边形FDEG是平行四边形,
∴H为EF的中点.
∵DE=CE,
∴∠CDE=∠DCE=x°,
∵∠CDE=∠DEH=
| 1 |
| 2 |
∴∠deh=x°,∠HEC=2x°,
∵∠CDE+∠DEC+∠DCE=180°,
∴5x=180°,
x=36°,
∵DE⊥BD,
∴∠EDB=90°,
∴∠BDC=90°-36°=54°,
∵四边形ABCD是矩形,
∴AB∥CD,
∴∠ABG=∠BDC=54°;
(2)证明:

连接AC,GE,
∵四边形ABCD是矩形,
∴AC=BD,AG=GC,BG=GD,
∴GD=GC,
∴G在CD的垂直平分线上,
∵DE=CE,
∴E在CD的垂直平分线上,
∴GE为CD的垂直平分线,
∴DM=CM,
∵BG=DG,
∴GM∥BC,
∴∠DGE=∠DBC,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DBC=∠FDG,
∴∠DGE=∠FDG,
∴FD∥GE,
∵FG⊥BD,DE⊥BD,
∴FG∥DE,
∴四边形FDEG是平行四边形,
∴H为EF的中点.
点评:本题考查了矩形的性质,等腰三角形的性质,平行四边形的性质和判定,线段垂直平分线性质的应用,主要考查学生综合运用性质进行推理的能力.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
某人走一段山路,山路长S千米,他先上山,速度a千米/时,再下山,速度为b千米/时,则他爬山平均速度为( )千米/时.
A、
| ||
B、
| ||
C、
| ||
D、
|
下列说法中正确的是( )
| A、想了解某种饮料中含色素的情况,宜采用抽样调查 |
| B、“打开电视,正在播放《新闻联播》”是必然事件 |
| C、数据1,1,2,2,3的众数是3 |
| D、一组数据的波动越大,方差越小 |
 如图,在△ABC中,点D、E分别在AB、AC上,DE∥BC.若AD=4,DB=2,则
如图,在△ABC中,点D、E分别在AB、AC上,DE∥BC.若AD=4,DB=2,则| DE |
| BC |
A、
| ||
B、
| ||
C、
| ||
| D、2 |
在2,O,-
,-1四个数中最小是( )
| 1 |
| 2 |
| A、0 | ||
B、
| ||
| C、-1 | ||
| D、2 |
