题目内容
如图,平面直角坐标系xOy中,一次函数y=- x+b(b为常数,b>0)的图象与x轴、y轴分别相交于点A、B,半径为4的⊙O与x轴正半轴相交于点C,与y轴相交于点D、E,点D在点E上方.
x+b(b为常数,b>0)的图象与x轴、y轴分别相交于点A、B,半径为4的⊙O与x轴正半轴相交于点C,与y轴相交于点D、E,点D在点E上方.

(1)若直线AB与 有两个交点F、G.
有两个交点F、G.
①求∠CFE的度数;
②用含b的代数式表示FG2,并直接写出b的取值范围;
(2)设b≥5,在线段AB上是否存在点P,使∠CPE=45°?若存在,请求出P点坐标;若不存在,请说明理由.
(1)45°; FG2=64×(1- )(4≤b<5);(2)不存在,理由见解析.
)(4≤b<5);(2)不存在,理由见解析.
【解析】
试题分析:(1)连接CD,EA,利用同一条弦所对的圆周角相等求行∠CFE=45°,
(2)作OM⊥AB点M,连接OF,利用两条直线垂直相交求出交点M的坐标,利用勾股定理求出FM2,再求出FG2,再根据式子写出b的范围,
(3)当b=5时,直线与圆相切,存在点P,使∠CPE=45°,再利用△APO∽△AOB和△AMP∽△AOB相似得出点P的坐标,再求出OP所在的直线解析式.
试题解析:(1)①如图1,
∵∠COE=90°
∴∠CFE= ∠COE=45°;
∠COE=45°;
如图2,作OM⊥AB点M,连接OF,

∵OM⊥AB,直线的函数式为:y=- x+b,
x+b,
∴OM所在的直线函数式为:y= x,
x,
∴交点M( ,
, )
)
∴OM2=( )2+(
)2+( )2,
)2,
∵OF=4,
∴FM2=OF2-OM2=42-( )2-(
)2-( )2,
)2,
∵FM= FG,
FG,
∴FG2=4FM2=4×[42-( )2-(
)2-( )2]=64-
)2]=64-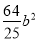 =64×(1-
=64×(1- ),
),
∵直线AB与 有两个交点F、G.
有两个交点F、G.
∴4≤b<5,
∴FG2=64×(1- )(4≤b<5)
)(4≤b<5)
(2)如图,

当b=5时,直线与圆相切,
∵在直角坐标系中,∠COE=90°,
∴∠CPE=∠ODC=45°,
∴存在点P,使∠CPE=45°,
连接OP,
∵P是切点,
∴OP⊥AB,
∴△APO∽△AOB,
∴ ,
,
∵OP=r=4,OB=5,AO= ,
,
∴
即AP= ,
,
∵AB= =
= ,
,
作PM⊥AO交AO于点M,设P的坐标为(x,y),
∵△AMP∽△AOB,
∴
∴ ,
,
∴y= ,
,
∴x=OM=
∴点P的坐标为( ,
, ).
).
当b>5时,直线与圆相离,不存在P点.
考点:圆的综合题.



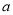 -2(3
-2(3 -5)=5+a-6
-5)=5+a-6 +10
+10 

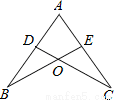
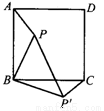
 D.
D.