题目内容
如图,抛物线y=ax2+bx+c经过A (-1,0)、B (3,0)、C (0,3)三点,对称轴与抛物线相交于点P、与直线BC相交于点M.

(1)求该抛物线的解析式: ;
(2)在BC上方的抛物线上是否存在一点K,使四边形ABKC的面积最大?若存在,求出K点的坐标及最大面积;
(3)连接CP,在第一象限的抛物线上是否存在一点R,使△RPM与△RMB的面积相等?若存在,求出点R的坐标;若不存在,说明理由.

(1)求该抛物线的解析式:
(2)在BC上方的抛物线上是否存在一点K,使四边形ABKC的面积最大?若存在,求出K点的坐标及最大面积;
(3)连接CP,在第一象限的抛物线上是否存在一点R,使△RPM与△RMB的面积相等?若存在,求出点R的坐标;若不存在,说明理由.
考点:二次函数综合题
专题:
分析:(1)把三点坐标代入函数式,列式求得a,b,c的值,即求出解析式;
(2)设存在点K,使得四边形ABKC的面积最大,根据点K在抛物线y=-x2+2x+3上设点K的坐标为:(x,-x2+2x+3),根据S四边形ABKC=S△AOC+S梯形ONKC+S△BNK得到有关x的二次函数求得最大值即可.
(3)求得点M,由点M,P的纵坐标关系可知,点R存在,y=2代入解得.
(2)设存在点K,使得四边形ABKC的面积最大,根据点K在抛物线y=-x2+2x+3上设点K的坐标为:(x,-x2+2x+3),根据S四边形ABKC=S△AOC+S梯形ONKC+S△BNK得到有关x的二次函数求得最大值即可.
(3)求得点M,由点M,P的纵坐标关系可知,点R存在,y=2代入解得.
解答:解:(1)把三点代入抛物线解析式
即得:
所以二次函数式为y=-x2+2x+3;
 (2)设存在点K,使得四边形ABKC的面积最大
(2)设存在点K,使得四边形ABKC的面积最大
∵点K在抛物线y=-x2+2x+3上,
∴设点K的坐标为:(x,-x2+2x+3),
作KN⊥AB于点N,
根据题意得:AO=1,OC=3,ON=x,BN=3-x,KN=-x2+2x+3,
∴S四边形ABKC=S△AOC+S梯形ONKC+S△BNK
=
AO•CO+
(OC+KN)•ON+
KN•BN
=
×1×3+
×(3-x2+2x+3)•x+
×(x-3)(-x2+2x+3)
=-
x2+
x+6
=-
(x-
)2+
,
∵x=
时,-x2+2x+3=-
+2×
+3=
,
∴在BC上方的抛物线上存在一点K(
,
),使四边形ABKC的面积最大,最大面积为
;
(3)由题意求得直线BC代入x=1,则y=2,
∴M(1,2),
由点M,P的坐标可知:
点R存在,即过点M平行于x轴的直线,
则代入y=2,x2-2x-1=0,
解得x=1-
(在对称轴的左侧,舍去),x=1+
,即点R(1+
,2).
|
即得:
|
所以二次函数式为y=-x2+2x+3;
 (2)设存在点K,使得四边形ABKC的面积最大
(2)设存在点K,使得四边形ABKC的面积最大∵点K在抛物线y=-x2+2x+3上,
∴设点K的坐标为:(x,-x2+2x+3),
作KN⊥AB于点N,
根据题意得:AO=1,OC=3,ON=x,BN=3-x,KN=-x2+2x+3,
∴S四边形ABKC=S△AOC+S梯形ONKC+S△BNK
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=-
| 3 |
| 2 |
| 9 |
| 2 |
=-
| 3 |
| 2 |
| 3 |
| 2 |
| 75 |
| 8 |
∵x=
| 3 |
| 2 |
| 9 |
| 4 |
| 3 |
| 2 |
| 15 |
| 4 |
∴在BC上方的抛物线上存在一点K(
| 3 |
| 2 |
| 15 |
| 4 |
| 75 |
| 8 |
(3)由题意求得直线BC代入x=1,则y=2,
∴M(1,2),
由点M,P的坐标可知:
点R存在,即过点M平行于x轴的直线,
则代入y=2,x2-2x-1=0,
解得x=1-
| 2 |
| 2 |
| 2 |
点评:本题考查了二次函数的综合运用,考查到了三点确定二次函数解析式;点M的纵坐标的长度是点P的一半,从而解得.本题逻辑思维性强,需要耐心和细心,是道好题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
⊙O1的半径为1,⊙O2的半径为8,两圆的圆心距为7,则两圆的位置关系为( )
| A、相交 | B、内切 | C、相切 | D、外切 |
下列各数中属于正整数的是( )
| A、1 | ||
| B、0 | ||
C、
| ||
D、
|
抛物线y=ax2-2x-a+1的对称轴是直线x=1,则a的值是( )
| A、-2 | B、2 | C、-1 | D、1 |
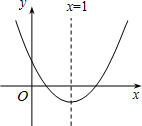 二次函数y=ax2+bx+c的图象,如图所示,其对称轴为直线x=1,若点A(-1,y1),B(2,y2)是它图象上的两点,则y1与y2的大小关系是( )
二次函数y=ax2+bx+c的图象,如图所示,其对称轴为直线x=1,若点A(-1,y1),B(2,y2)是它图象上的两点,则y1与y2的大小关系是( )| A、y1<y2 |
| B、y1=y2 |
| C、y1>y2 |
| D、不能确定 |
 如图,村庄B在村庄A的
如图,村庄B在村庄A的