题目内容
有理数a，b，c满足|a+b+c|=a-b+c，且b≠0，则|a-b+c+1|-|b-2|的值为 ．
考点：绝对值
专题：
分析：根据|a+b+c|=a-b+c，可得a-b+c≥0，a+c=0，b＜0，然后代入求解即可．
解答：解：∵|a+b+c|=a-b+c，
∴a-b+c≥0，a+c=0，b＜0，
则|a-b+c+1|-|b-2|=a-b+c+1+b-2=a+c-1．
故答案为：a+c-1．
∴a-b+c≥0，a+c=0，b＜0，
则|a-b+c+1|-|b-2|=a-b+c+1+b-2=a+c-1．
故答案为：a+c-1．
点评：本题考查了绝对值的知识，解答本题的关键是掌握绝对值的性质，进行绝对值的化简．
练习册系列答案
相关题目
如图，点P（x，y）（x＞0）是反比例函数y=| k |
| x |
| A、S的值增大 |
| B、S的值减小 |
| C、S的值先增大，后减小 |
| D、S的值不变 |
若∠A的余角是它的7倍，则∠A的度数等于（ ）
| A、11°2′5″ |
| B、11°15′ |
| C、11°25′ |
| D、11°12′30″ |
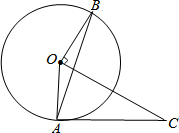如图△AOC中，以O为圆心，OA为半径作⊙O，作OB⊥OC交⊙O于点B，垂足为点O，连接AB交OC于点D，∠CAD=∠CDA．（1）求证：AC是⊙O的切线；
（2）若OA=5，OD=1，求线段AC的长．
已知点P（x，y） 是第三象限内的一点，且x2=4，|y|=3，则P点的坐标是（ ）
| A、（-2，-3） |
| B、（2，3） |
| C、（-2，3） |
| D、（2，-3） |
已知a、b、c是△ABC的三边的长，且满足a2+2b2+c2-2b（a+c）=0，此三角形的形状是（ ）
| A、等腰三角形 |
| B、不等边三角形 |
| C、等边三角形 |
| D、等腰直角三角形 |