题目内容
13. 如图,在△ABC中,BD1平分∠ABC,CD1平分△ABC的外角∠ACE,BD1,CD1相交于D1.
如图,在△ABC中,BD1平分∠ABC,CD1平分△ABC的外角∠ACE,BD1,CD1相交于D1.(1)若∠A=96°,求出∠D1的度数;
(2)若∠A=α,∠D1BC与∠D1CE的平分线相交于点D2,依此类推,∠Dn-1BC与∠Dn-1CE的平分线相交于点Dn,请直接写出∠Dn的度数.
分析 (1)根据角平分线定义得出∠ABC=2∠DBC,∠ACE=2∠DCE,根据三角形外角性质得出2∠D+∠ABC=∠A+∠ABC,求出∠A=2∠D,即可求出答案;
(2)根据(1)的过程可得出结论.
解答 解:(1)∵BD平分∠ABC,CD1平分∠ACE,
∴∠ABC=2∠D1BC,∠ACE=2∠D1CE,
∵∠ACE=2∠D1CE=∠A+∠ABC,∠D1CE=∠D1+∠D1BC,
∴2∠D1CE=2∠D1+2∠D1BC,
∴∠ACE=2∠D1+∠ABC,
∴2∠D1+∠ABC=∠A+∠ABC,
∴∠A=2∠D1,
∵∠A=96°,
∴∠D1=$\frac{1}{2}$∠A=48°;
(2)由(1)的结论可知,∠D1=$\frac{1}{2}$∠A,
同理可得,∠D2=$\frac{1}{{2}^{2}}$∠A,
故∠Dn=$\frac{1}{{2}^{n}}$∠A.
点评 本题考查的是三角形内角和定理,熟知三角形的内角和等于360°是解答此题的关键.

练习册系列答案
相关题目
5.已知|3x+4|+y2-6y+9=0,则xy的值是( )
| A. | 4 | B. | -4 | C. | $\frac{9}{4}$ | D. | -$\frac{9}{4}$ |
3.已知(m-n)2=10,(m+n)2=2,则m2+n2=( )
| A. | 3 | B. | 5 | C. | 6 | D. | 10 |
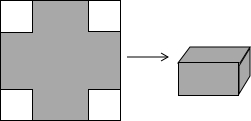 你能用正方形纸片制作长方体纸盒吗?如图,在正方形的四个角剪下同样大小的四个小正方形,把剩下的纸片折叠成一个无盖的纸盒,然后把剪下的四个小正方形纸片拼成一个大正方形作为纸盒的盖.如果我们希望做成的长方体的体积为4cm3,那么用作原料的大正方形纸片的边长应是多少.
你能用正方形纸片制作长方体纸盒吗?如图,在正方形的四个角剪下同样大小的四个小正方形,把剩下的纸片折叠成一个无盖的纸盒,然后把剪下的四个小正方形纸片拼成一个大正方形作为纸盒的盖.如果我们希望做成的长方体的体积为4cm3,那么用作原料的大正方形纸片的边长应是多少.