题目内容
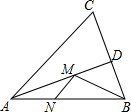 如图,在锐角△ABC中,AB=
如图,在锐角△ABC中,AB=| 2 |
A、
| ||||
| B、1 | ||||
C、
| ||||
D、
|
考点:轴对称-最短路线问题
专题:
分析:作BH⊥AC,垂足为H,交AD于M′点,过M′点作M′N′⊥AB,垂足为N′,则BM′+M′N′为所求的最小值,再根据AD是∠BAC的平分线可知M′H=M′N′,再由锐角三角函数的定义即可得出结论.
解答: 解:如图,作BH⊥AC,垂足为H,交AD于M′点,过M′点作M′N′⊥AB,垂足为N′,则BM′+M′N′为所求的最小值.
解:如图,作BH⊥AC,垂足为H,交AD于M′点,过M′点作M′N′⊥AB,垂足为N′,则BM′+M′N′为所求的最小值.
∵AD是∠BAC的平分线,
∴M′H=M′N′,
∴BH是点B到直线AC的最短距离(垂线段最短),
∵AB=
,∠BAC=45°,
∴BH=AB•sin45°=
×
=1.
∵BM+MN的最小值是BM′+M′N′=BM′+M′H=BH=1.
故选B.
 解:如图,作BH⊥AC,垂足为H,交AD于M′点,过M′点作M′N′⊥AB,垂足为N′,则BM′+M′N′为所求的最小值.
解:如图,作BH⊥AC,垂足为H,交AD于M′点,过M′点作M′N′⊥AB,垂足为N′,则BM′+M′N′为所求的最小值.∵AD是∠BAC的平分线,
∴M′H=M′N′,
∴BH是点B到直线AC的最短距离(垂线段最短),
∵AB=
| 2 |
∴BH=AB•sin45°=
| 2 |
| ||
| 2 |
∵BM+MN的最小值是BM′+M′N′=BM′+M′H=BH=1.
故选B.
点评:本题考查的是轴对称-最短路线问题,解答此类问题时要从已知条件结合图形认真思考,通过角平分线性质,垂线段最短,确定线段和的最小值.

练习册系列答案
相关题目
已知点P在⊙O的内部,⊙O的半径为10cm,那么点P到⊙O的距离可以是( )
| A、9cm | B、10cm |
| C、11cm | D、12cm |
抛一枚质地均匀的骰子,向上一面的点数大于2且小于5的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
下列各点中不在抛物线y=
x2上的是( )
| 1 |
| 2 |
| A、(0,0) |
| B、(1,1) |
| C、(2,2) |
| D、(4,8) |
 △ABC在方格纸中的位置如图所示,方格纸中的每个小正方形的边长为1个单位,
△ABC在方格纸中的位置如图所示,方格纸中的每个小正方形的边长为1个单位,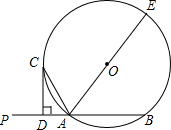 如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA,垂足为D.
如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA,垂足为D.