题目内容
14.等腰三角形的周长为10cm,其中一边长为2cm,则该等腰三角形底边上的高为( )| A. | 2$\sqrt{2}$ | B. | 4$\sqrt{2}$ | C. | $\sqrt{15}$ | D. | 4$\sqrt{2}$或$\sqrt{15}$ |
分析 分两种情况:①当底边bc为2cm时,AB=AC=4cm,由等腰三角形的性质得出BD=CD=$\frac{1}{2}$BC=1cm,由勾股定理求出AD即可;
②当腰长AB=AC=2cm时,底边BC=6cm,由三角形的三边关系得出不能构成三角形;即可得出结果.
解答 解:分两种情况:
①当底边bc为2cm时,如图所示:
∵等腰三角形的周长为10cm,
∴AB=AC=4cm,
∵AD是高,
∴BD=CD=$\frac{1}{2}$BC=1cm,∠ADB=90°,
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=$\sqrt{{4}^{2}-{1}^{2}}$=$\sqrt{15}$(cm);
②当腰长AB=AC=2cm时,底边BC=6cm,
∵2+2<6,
∴不能构成三角形;
综上所述:该等腰三角形底边上的高为$\sqrt{15}$;
故选:C.
点评 本题考查了勾股定理、等腰三角形的性质、三角形的三边关系;熟练掌握等腰三角形的性质和三角形的三边关系,运用勾股定理进行计算是解决问题的关键.

练习册系列答案
相关题目
2.①若a=-b,则|a|=|b|;
②若a<b,则|a|<|b|;
③无论m为什么数,m÷m=1;
④一个数前面加上“-”号,这个数就是负数;
⑤表示-2的点离原点2个单位长度.
以上说法错误的有②③④.
②若a<b,则|a|<|b|;
③无论m为什么数,m÷m=1;
④一个数前面加上“-”号,这个数就是负数;
⑤表示-2的点离原点2个单位长度.
以上说法错误的有②③④.
9.参加第十七届韩日世界杯足球赛的23名中国队员的年龄如表所示:
(1)求出年龄最大的队员与年龄最小的队员的年龄差;
(2)求出中国队队员的平均年龄.
| 21 | 29 | 24 | 27 | 33 | 22 | 25 | 25 | 32 | 31 | 28 | 31 |
| 24 | 24 | 23 | 21 | 20 | 27 | 26 | 28 | 23 | 34 | 34 |
(2)求出中国队队员的平均年龄.
 如图,AB是⊙O的直径,AD,DC,BC是切线,点A,E,B为切点
如图,AB是⊙O的直径,AD,DC,BC是切线,点A,E,B为切点 如图,这是一个由小立方块搭成的几何体的俯视图,小正方形中的数字表示在该位置的小立方块的个数.请你画出它的主视图与左视图.
如图,这是一个由小立方块搭成的几何体的俯视图,小正方形中的数字表示在该位置的小立方块的个数.请你画出它的主视图与左视图.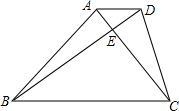 如图,在梯形ABCD中,AD∥BC,对角线AC与BD互相垂直,且BC-AD=4,cos∠DBC=0.8,AC=6.求BC的长及梯形的面积.
如图,在梯形ABCD中,AD∥BC,对角线AC与BD互相垂直,且BC-AD=4,cos∠DBC=0.8,AC=6.求BC的长及梯形的面积.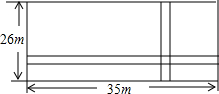 如图,在一块长35m,宽26m的矩形地面上修建同样宽的两条互相垂直的道路(两条道路各与矩形的一条边平行),剩余部分栽种花草,要使剩余部分的面积为850m2,道路的宽应该为多少?
如图,在一块长35m,宽26m的矩形地面上修建同样宽的两条互相垂直的道路(两条道路各与矩形的一条边平行),剩余部分栽种花草,要使剩余部分的面积为850m2,道路的宽应该为多少?