题目内容
4.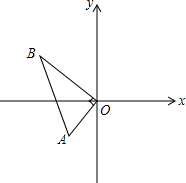 如图,在Rt△AOB中,∠AOB=90°,已知点A(-1,-1),点B在第二象限,OB=2$\sqrt{2}$,抛物线y=$\frac{3}{5}$x2+bx+c经过点A和B.
如图,在Rt△AOB中,∠AOB=90°,已知点A(-1,-1),点B在第二象限,OB=2$\sqrt{2}$,抛物线y=$\frac{3}{5}$x2+bx+c经过点A和B.(1)求点B的坐标;
(2)求抛物线y=$\frac{3}{5}$x2+bx+c的对称轴;
(3)如果该抛物线的对称轴分别和边AO、BO的延长线交于点C、D,设点E在直线AB上,当△BOE和△BCD相似时,直接写出点E的坐标.
分析 (1)根据互相垂直的两直线一次项系数的乘积为-1,可得BO的解析式,根据勾股定理,可得B点坐标;
(2)根据待定系数法,可得函数解析式,根据配方法,可得答案;
(3)根据待定系数,可得AB的解析式,根据自变量与函数值的对应关系,可得E、F点的坐标,分类讨论:△BCD∽△BEO时,可得F点坐标;△BCD∽△BOE时,根据相似于同一个三角形的两个三角形相似,可得△BFO∽BOE,根据相似三角形的性质,可得BF的长,根据勾股定理,可得F点坐标.
解答 解:(1)AO的解析式为y=x,AO⊥BO,
BO的解析式为y=-x,设B点坐标为(a,-a),
由OB=2$\sqrt{2}$,得
$\sqrt{{a}^{2}+(-a)^{2}}$=2$\sqrt{2}$.
解得a=2(不符合题意,舍),或a=-2,
B(-2,2);
(2)将A、B点坐标代入函数解析式,得
$\left\{\begin{array}{l}{\frac{3}{5}-b+c=-1}\\{\frac{3}{5}×4-2b+c=2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=-\frac{6}{5}}\\{c=-\frac{14}{5}}\end{array}\right.$,
y=$\frac{3}{5}$x2-$\frac{6}{5}$x-$\frac{14}{5}$=$\frac{3}{5}$(x-1)2-$\frac{17}{5}$,
对称轴是直线x=1;
(3)设AB的解析式为y=kx+b,
将A、B点的坐标代入,得
$\left\{\begin{array}{l}{-k+b=-1}\\{-2k+b=2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-3}\\{b=-4}\end{array}\right.$,
AB的解析式为y=-3x-4.
当y=0时,x=-$\frac{4}{3}$,即F(-$\frac{4}{3}$,0).
AO:y=x,当x=1时,y=1,即C(1,1);
BO:y=-x,当x=1时,y=-1,即D(1,-1);
AB=BC=$\sqrt{10}$,AO=OC=$\sqrt{2}$.
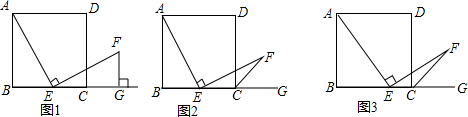
①图1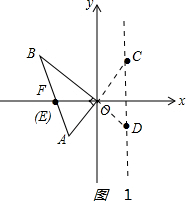 ,
,
∠CBD=∠ABD,∠BOF=∠BDC=45°,△BCD∽△BEO时.
此时,F与E重合,E(-$\frac{4}{3}$,0);
②图2 ,设E点坐标为(b,-3b-4),
,设E点坐标为(b,-3b-4),
△BCD∽△BOE时,
∵△BCD∽△BFO,
∴△BFO∽BOE,
$\frac{BO}{BE}$=$\frac{BF}{BO}$,
∴BO2=BF•BE,
8=$\frac{2\sqrt{10}}{3}$•BE,
BE=$\frac{6\sqrt{10}}{5}$,
$\sqrt{(b+2)^{2}+(-3b-4-2)^{2}}$=$\frac{6\sqrt{10}}{b}$,
解得b=-$\frac{4}{5}$,-3b-4=-3×(-$\frac{4}{5}$)-4=-$\frac{8}{5}$,
∴E(-$\frac{4}{5}$,-$\frac{8}{5}$),
综上所述:当△BOE和△BCD相似时,直接写出点E的坐标(-$\frac{4}{3}$,0),(-$\frac{4}{5}$,-$\frac{8}{5}$).
点评 本题考查了二次函数综合题,利用互相垂直的两直线一次项系数的乘积为-1得出BO的解析式是解题关键;利用配方法得出对称轴是解题关键;利用相似于同一个三角形的两个三角形相似得出△BFO∽BOE,又利用了相似三角形的性质.

| A. | 15 | B. | 115 | C. | 225 | D. | 625 |
| A. | -12 | B. | -7 | C. | -1 | D. | 1 |
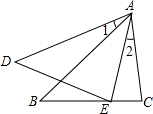 如图,已知∠1=∠2,∠AED=∠C,求证:△ABC∽△ADE.
如图,已知∠1=∠2,∠AED=∠C,求证:△ABC∽△ADE.