Question

（1）如图①，∠AOB=60°，OD平分∠BOC，OE平分∠AOC，求∠EOD的度数；
（2）若∠AOB=90°，其它条件不变，则∠EOD=

 

；
（3）若∠AOB=α，其它条件不变，则∠EOD=

 

；
（4）如图②，请你根据中点的知识编一道类似的题，并写出求解过程．

Answer 1

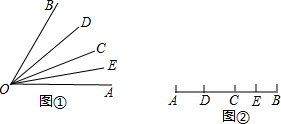
分析：（1）根据角平分线的定义，∠COD=

1

2

∠BOC，∠COE=

1

2

∠AOC，所以∠EOD=

1

2

∠AOB，代入数据计算即可；
（2）与（1）的求解与解答思路相同；
（3）与（1）的求解与解答思路相同；
（4）把题中的∠AOB换成线段AB，相应的角平分线换成中点即可．

解答：解：（1）∵OD平分∠BOC，OE平分∠AOC，
∴∠DOC=

1

2

∠BOC，∠COE=

1

2

∠AOC，
∴∠EOD=∠DOC+∠COE，
=

1

2

∠BOC+

1

2

∠AOC，
=

1

2

（∠BOC+∠AOC）
=

1

2

∠AOB，
∵∠AOB=60°，
∴∠EOD=

1

2

×60°=30°；

（2）同理∠EOD=

1

2

∠AOB=

1

2

×90°=45°；

（3）同理∠EOD=

1

2

∠AOB=

α

2

；

（4）如图②，已知AB=a，C是线段AB上任意一点，D是AC的中点，E是BC的中点，求DE的长．
解答：∵D是AC的中点，E是BC的中点，
∴DC=

1

2

AC，EC=

1

2

BC；
∴DE=

1

2

AC+

1

2

BC=

1

2

（AC+BC）=

1

2

AB=

a

2

．

点评：本题主要利用角平分线的定义求解，熟练掌握概念是解题的关键，还考查了同学们对于知识的转移能力．