题目内容
5.解不等式组$\left\{\begin{array}{l}{2x+1>x-5①}\\{4x≤3x+2②}\end{array}\right.$请结合题意填空,完成本小题的解答.
(1)解不等式①,得x>-6;
(2)解不等式②,得x≤2;
(3)把不等式①和②的解集在数轴上表示出来;
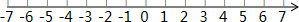
(4)原不等式组的解集为-6<x≤2.
分析 (1)先移项,再合并同类项,求出不等式①的解集即可;
(2)先移项,再合并同类项,求出不等式②的解集即可;
(3)把两不等式的解集在数轴上表示出来即可;
(4)根据数轴上不等式的解集,求出其公共部分即可.
解答 解:(1)解不等式①得,x>-6.
故答案为:x>-6;
(2)解不等式②得,x≤2.
故答案为:x≤2;
(3)不等式①和②的解集在数轴上表示为: ;
;
(4)由(3)得,不能等式组的解集为:-6<x≤2.
故答案为:-6<x≤2.
点评 本题考查的是解一元一次不等式组,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
17.解二元一次方程组的基本思想是( )
| A. | 代入法 | |
| B. | 加减法 | |
| C. | 消元,化二元为一元 | |
| D. | 由一个未知数的值求另一个未知数的值 |
15.方程(m-2)x|m|-1-2=0是关于x的一元一次方程,则m的值为( )
| A. | -2 | B. | 2 | C. | -1 | D. | 2或-2 |
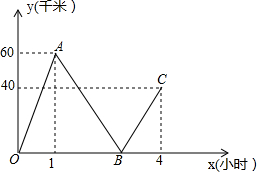 甲、乙两车先后从M地驶向N地,甲车出发一小时后,乙车出发,用了两个小时追上甲车,乙车此时马上改变速度又用了1小时到达N地.图中折线表示两车距离y(千米)与甲车行驶时间x(小时)之间的函数关系(0≤x≤4).甲、乙两车匀速行驶.请根据图象信息解答下列问题:
甲、乙两车先后从M地驶向N地,甲车出发一小时后,乙车出发,用了两个小时追上甲车,乙车此时马上改变速度又用了1小时到达N地.图中折线表示两车距离y(千米)与甲车行驶时间x(小时)之间的函数关系(0≤x≤4).甲、乙两车匀速行驶.请根据图象信息解答下列问题: