题目内容
8. 如图,在Rt△ABC中,∠C=90°,∠BAC=60°,∠BAC的平分线AM长为8cm,求BC的长.
如图,在Rt△ABC中,∠C=90°,∠BAC=60°,∠BAC的平分线AM长为8cm,求BC的长.
分析 因为AM是∠BAC的平分线,∠BAC=60°,在Rt△ACM中,可利用勾股定理求得MC,进一步求得AC;求得∠ABC=30°,在Rt△ABC中,可求得AB,最后利用勾股定理求出BC.
解答 解:∵AM是∠BAC的平分线,∠BAC=60°,
∴∠MAC=30°,
∴MC=$\frac{1}{2}$AM=4cm,
∴AC=$\sqrt{A{M}^{2}-M{C}^{2}}$=$\sqrt{{8}^{2}-{4}^{2}}$=4$\sqrt{3}$,
∵在△ABC中,∠C=90°,∠BAC=60°,
∴∠ABC=30°,
∴AB=2AC=8$\sqrt{3}$,
∴BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=12.
点评 本题考查了角平分线的定义,含30°直角三角形的性质,勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.用边长为4cm,5cm,6cm的两个全等三角形拼成四边形,一共能拼成( )个平行四边形.
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
18.下列各式中正确的是( )
| A. | $\sqrt{5}$<2 | B. | -4>-$\sqrt{15}$ | C. | 1-$\sqrt{2}$<0 | D. | $\sqrt{16}$<$\sqrt{8}$ |



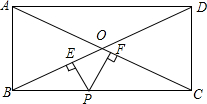 矩形ABCD中,AB=6,BC=8,P是BC边上的一点,PE⊥BD,PF⊥AC,垂足分别为E,F.求证:PE+PF为定值.
矩形ABCD中,AB=6,BC=8,P是BC边上的一点,PE⊥BD,PF⊥AC,垂足分别为E,F.求证:PE+PF为定值. 如图:计算下面各个图形的表面积与体积.
如图:计算下面各个图形的表面积与体积. 如图所示,已知等边三角形ABC的外接圆⊙O的半径为R,求△ABC的边长a、周长P、边心距r及面积S.
如图所示,已知等边三角形ABC的外接圆⊙O的半径为R,求△ABC的边长a、周长P、边心距r及面积S.