题目内容
若等腰三角形有两条边的长度为3和1,则此等腰三角形的周长= ;若直角三角形斜边上的中线长5cm,斜边上的高是4cm,则它的面积= cm2.
考点:等腰三角形的性质,三角形三边关系,直角三角形斜边上的中线
专题:
分析:因为已知长度为3和1两边,没由明确是底边还是腰,所以有两种情况,需要分类讨论;
根据直角三角形斜边上的中线等于斜边的一半求出斜边,然后根据三角形的面积公式列式计算即可得解.
根据直角三角形斜边上的中线等于斜边的一半求出斜边,然后根据三角形的面积公式列式计算即可得解.
解答:解:当3为底时,其它两边都为1,
∵1+1<3,
∴不能构成三角形,故舍去,
当3为腰时,
其它两边为3和1,
3、3、1可以构成三角形,
周长为7.
∵直角三角形斜边上中线长5cm,
∴斜边=2×5=10cm,
∴面积=
×10×4=20cm2.
故答案是:7;20.
∵1+1<3,
∴不能构成三角形,故舍去,
当3为腰时,
其它两边为3和1,
3、3、1可以构成三角形,
周长为7.
∵直角三角形斜边上中线长5cm,
∴斜边=2×5=10cm,
∴面积=
| 1 |
| 2 |
故答案是:7;20.
点评:考查了等腰三角形的性质和三角形的三边关系;已知没有明确腰和底边的题目一定要想到两种情况,分类进行讨论,还应验证各种情况是否能构成三角形进行解答,这点非常重要,也是解题的关键.同时考查了直角三角形斜边上的中线等于斜边的一半的性质,三角形的面积,熟记性质求出斜边的长度是解题的关键.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目

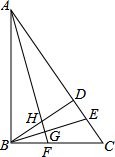 如图,在Rt△ABC中,∠ABC=90°,过点B作BD⊥AC于D,BE平分∠DBC,交AC于E,过点A作AF⊥BE于G,交BC于F,交BD于H.若∠BAC=30°,则
如图,在Rt△ABC中,∠ABC=90°,过点B作BD⊥AC于D,BE平分∠DBC,交AC于E,过点A作AF⊥BE于G,交BC于F,交BD于H.若∠BAC=30°,则