题目内容
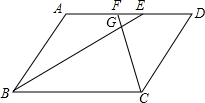 如图,在?ABCD中,∠ABC、∠BCD的平分线BE、CF分别与AD相交于点E、F,BE与CF相交于点G.
如图,在?ABCD中,∠ABC、∠BCD的平分线BE、CF分别与AD相交于点E、F,BE与CF相交于点G.(1)求证:BE⊥CF;
(2)若AB=3,BC=5,CF=2,求BE的长.
考点:平行四边形的性质
专题:
分析:(1)根据平行四边形两组对边分别平行可得∠ABC+∠BCD=180°,再根据角平分线的性质可得∠EBC+∠FCB=
∠ABC+
∠DCB=90°,进而可得BE⊥CF;
(2)过A作AM∥FC,首先证明△ABE是等腰三角形,进而得到BO=EO,再利用勾股定理计算出EO的长,进而可得答案.
| 1 |
| 2 |
| 1 |
| 2 |
(2)过A作AM∥FC,首先证明△ABE是等腰三角形,进而得到BO=EO,再利用勾股定理计算出EO的长,进而可得答案.
解答: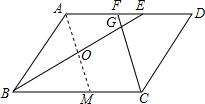 (1)证明:∵四边形ABCD是平行四边形,
(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠ABC+∠BCD=180°,
∵∠ABC、∠BCD的平分线BE、CF分别与AD相交于点E、F,
∴∠EBC+∠FCB=
∠ABC+
∠DCB=90°,
∴EB⊥FC;
(2)解:过A作AM∥FC,
∵AM∥FC,
∴∠AOB=∠FGB,
∵EB⊥FC,
∴∠FGB=90°,
∴∠AOB=90°,
∵BE平分∠ABC,
∴∠ABE=∠EBC,
∵AD∥BC,
∴∠AEB=∠CBE,
∴∠ABE=∠AEB,
∴AB=AE=3,
∵AO⊥BE,
∴BO=EO,
在△AOE和△MOB中
,
∴△AOE≌△MOB(ASA),
∴AO=MO,
∵AF∥CM,AM∥FC,
∴四边形AMCF是平行四边形,
∴AM=FC=2,
∴AO=1,
∴EO=
=2
,
∴BE=4
.
 (1)证明:∵四边形ABCD是平行四边形,
(1)证明:∵四边形ABCD是平行四边形,∴AB∥CD,
∴∠ABC+∠BCD=180°,
∵∠ABC、∠BCD的平分线BE、CF分别与AD相交于点E、F,
∴∠EBC+∠FCB=
| 1 |
| 2 |
| 1 |
| 2 |
∴EB⊥FC;
(2)解:过A作AM∥FC,
∵AM∥FC,
∴∠AOB=∠FGB,
∵EB⊥FC,
∴∠FGB=90°,
∴∠AOB=90°,
∵BE平分∠ABC,
∴∠ABE=∠EBC,
∵AD∥BC,
∴∠AEB=∠CBE,
∴∠ABE=∠AEB,
∴AB=AE=3,
∵AO⊥BE,
∴BO=EO,
在△AOE和△MOB中
|
∴△AOE≌△MOB(ASA),
∴AO=MO,
∵AF∥CM,AM∥FC,
∴四边形AMCF是平行四边形,
∴AM=FC=2,
∴AO=1,
∴EO=
| AE2-AO2 |
| 2 |
∴BE=4
| 2 |
点评:此题主要考查了平行四边形的性质,以及等腰三角形的判定和性质,关键是证明出AO=MO,BO=EO.

练习册系列答案
相关题目
 已知:如图,AB=CD,AE=DF,且AE⊥BC于E,DF⊥BC于F.求证:∠B=
已知:如图,AB=CD,AE=DF,且AE⊥BC于E,DF⊥BC于F.求证:∠B= 如图所示,平移△ABC,使得顶点A平移到O处,再把所得到的三角形以点O为旋转中心按逆时针方向旋转90°,画出平移和旋转后得到的两个图形.
如图所示,平移△ABC,使得顶点A平移到O处,再把所得到的三角形以点O为旋转中心按逆时针方向旋转90°,画出平移和旋转后得到的两个图形.