题目内容
已知在平面直角坐标系xOy中,O是坐标原点,以P(1,1)为圆心的⊙P与x轴,y轴分别相切于点M和点N,点F从点M出发,沿x轴正方向以每秒1个单位长度的速度运动,连接PF,过点PE⊥PF交y轴于点E,设点F运动的时间是t秒(t>0)
(1)若点E在y轴的负半轴上(如图所示),求证:PE=PF;
(2)在点F运动过程中,设OE=a,OF=b,试用含a的代数式表示b;
(3)作点F关于点M的对称点F′,经过M、E和F′三点的抛物线的对称轴交x轴于点Q,连接QE.在点F运动过程中,是否存在某一时刻,使得以点Q、O、E为顶点的三角形与以点P、M、F为顶点的三角形相似?若存在,请直接写出t的值;若不存在,请说明理由.

解答:
证明:(1)如图,连接PM,PN,
∵⊙P与x轴,y轴分别相切于点M和点N,
∴PM⊥MF,PN⊥ON且PM=PN,
∴∠PMF=∠PNE=90°且∠NPM=90°,∵PE⊥PF,
 ∠NPE=∠MPF=90°﹣∠MPE,
∠NPE=∠MPF=90°﹣∠MPE,
在△PMF和△PNE中, ,∴△PMF≌△PNE(ASA),
,∴△PMF≌△PNE(ASA),
∴PE=PF,
(2)解:①当t>1时,点E在y轴的负半轴上,如图,
由(1)得△PMF≌△PNE,∴NE=MF=t,PM=PN=1,
∴b=OF=OM+MF=1+t,a=NE﹣ON=t﹣1,
∴b﹣a=1+t﹣(t﹣1)=2,∴b=2+a,
 ②0<t≤1时,如图2,点E在y轴的正半轴或原点上,
②0<t≤1时,如图2,点E在y轴的正半轴或原点上,
同理可证△PMF≌△PNE,
∴b=OF=OM+MF=1+t,a=ON﹣NE=1﹣t,
∴b+a=1+t+1﹣t=2,
∴b=2﹣a,
(3)如图3,(Ⅰ)当1<t<2时,
∵F(1+t,0),F和F′关于点M对称,
∴F′(1﹣t,0)
∵经过M、E和F′三点的抛物线的对称轴交x轴于点Q,
∴Q(1﹣ t,0)∴OQ=1﹣
t,0)∴OQ=1﹣ t,
t,
 由(1)得△PMF≌△PNE
由(1)得△PMF≌△PNE
∴NE=MF=t,∴OE=t﹣1
当△OEQ∽△MPF∴ =
= ∴
∴ =
= ,
,
解得,t= ,当△OEQ∽△MFP时,∴
,当△OEQ∽△MFP时,∴ =
= ,
,
 =
= ,解得,t=
,解得,t= ,
,
(Ⅱ)如图4,当t>2时,

∵F(1+t,0),F和F′关于点M对称,
∴F′(1﹣t,0)
∵经过M、E和F′三点的抛物线的对称轴交x轴于点Q,
∴Q(1﹣ t,0)∴OQ=
t,0)∴OQ= t﹣1,
t﹣1,
由(1)得△PMF≌△PNE ∴NE=MF=t,∴OE=t﹣1
当△OEQ∽△MPF∴ =
= ∴
∴ =
= ,无解,
,无解,
当△OEQ∽△MFP时,∴ =
= ,
, =
= ,解得,t=2±
,解得,t=2± ,
,
所以当t= ,t=
,t= ,t=2±
,t=2± 时,使得以点Q、O、E为顶点的三角形与以点P、M、F为顶点的三角形相似.
时,使得以点Q、O、E为顶点的三角形与以点P、M、F为顶点的三角形相似.


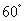 ,半径为
,半径为 ,则图中弓形的面积为( )
,则图中弓形的面积为( ) B.
B. C.
C. D.
D.

 ]
] =8,且圆O到直线AB的距离为6,求AC的长.
=8,且圆O到直线AB的距离为6,求AC的长.
 2,1,2,1,4,6中正确的是( )
2,1,2,1,4,6中正确的是( ) ,
, ,∠DAE=30°,作AE⊥AF交BC于F,则BF=( )
,∠DAE=30°,作AE⊥AF交BC于F,则BF=( ) C.
C.  D.
D. 

 (单位:平方米)与工作时间
(单位:平方米)与工作时间 (单位:小时)的函数关系的图象如图所示,则休息后园林队每小时绿化面积为
(单位:小时)的函数关系的图象如图所示,则休息后园林队每小时绿化面积为
 ,求cos∠DAB.
,求cos∠DAB.