题目内容
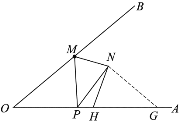
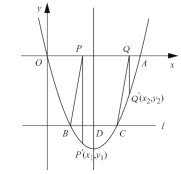
【题目】如图,AB是半圆O的直径,半径OC⊥AB于点O,点D是![]() 的中点,连接CD、OD.下列四个结论:①AC
的中点,连接CD、OD.下列四个结论:①AC![]() OD;②CE=OE;③△ODE∽△ADO;④∠ADC=∠BOD.其中正确结论的序号是( )
OD;②CE=OE;③△ODE∽△ADO;④∠ADC=∠BOD.其中正确结论的序号是( )
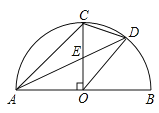
A.①④B.①②④C.②③D.①②③④
【答案】A
【解析】
如图,利用圆周角定理得∠1=∠3,加上∠1=∠2,则∠2=∠3,于是可对①进行判断;利用AC∥OD可判定△ACE∽△DOE,则![]() ,再判定△AOC为等腰直角三角形得到AC=
,再判定△AOC为等腰直角三角形得到AC=![]() OA=
OA=![]() OD,所以CE=
OD,所以CE=![]() OE,于是可对②进行判断;利用圆周角定理得到∠COD=2∠1,则根据相似三角形的判定方法可对③进行判断;利用圆周角定理可计算出∠ADC=45°,而∠BOD=45°,则可对④进行判断.
OE,于是可对②进行判断;利用圆周角定理得到∠COD=2∠1,则根据相似三角形的判定方法可对③进行判断;利用圆周角定理可计算出∠ADC=45°,而∠BOD=45°,则可对④进行判断.
解:如图,
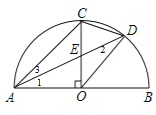
∵点D是![]() 的中点,
的中点,
即![]() ,
,
∴∠1=∠3,
∵OA=OD,
∴∠1=∠2,
∴∠2=∠3,
∴AC∥OD,所以①正确;
∴△ACE∽△DOE,
∴![]() ,
,
∵OC⊥OA,
∴△AOC为等腰直角三角形,
∴AC=![]() OA=
OA=![]() OD,
OD,
∴![]()
∴CE=![]() OE,所以②错误;
OE,所以②错误;
∵点D是![]() 的中点,
的中点,
∴∠BOD=∠COD
∵∠BOD=2∠1
∴∠COD=2∠1,
而∠ODE=∠ADO,
∴△ODE与△ADE不相似,所以③错误;
∵∠ADC=![]() ∠AOC=45°,∠BOD=
∠AOC=45°,∠BOD=![]() ∠BOC=45°,
∠BOC=45°,
∴∠ADC=∠BOD,所以④正确.
∴正确的结论是①④,
故选:A.

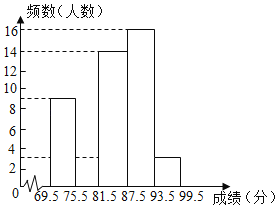
【题目】我市要开展“不忘初心,牢记使命”主题演讲比,某中学将参加本校选拔赛的50名选手的成绩(满分为100分,得分为正整数)分成五组,并绘制了不完整的统计图表.
分数段 | 频数 | 频率 |
69.5~75.5 | 9 | 0.18 |
75.5~81.5 | m | 0.16 |
81.5~87.5 | 14 | 0.28 |
87.5~93.5 | 16 | n |
93.5~99.5 | 3 | 0.06 |
(1)表中n= ,并在图中补全频数直方图.
(2)甲同学的比赛成绩是50位参赛选手成绩的中位数,据此推测他的成绩落在 分数段内;
(3)选拔赛时,成绩在93.5~99.5的三位选手中,男生2人,女生1人,学校从中随机确定2名选手参加全市决赛,请用列表法或树状图法求恰好是一名男生和一名女生的概率.