题目内容
8.从2、5、8、11、14…这一列数中取8个不同的数,使它们的倒数和是1,这8个数可以是多少?分析 首先判断出2、5、8、11、14…这一列数是以2为首项,3为公差的等差数列;然后选取倒数值最大的,即$\frac{1}{2}$;再选择$\frac{1}{5}$以及与$\frac{1}{5}$相加后可以约分的,即$\frac{1}{5}和$$\frac{1}{20}$;再选择$\frac{1}{14}$以及与$\frac{1}{14}$相加后可以约分的,即$\frac{1}{14}$和$\frac{1}{35}$;再选择$\frac{1}{41}$以及与$\frac{1}{41}$相加后可以约分的,即$\frac{1}{41}$和$\frac{1}{1640}$;最后确定出这8个数可以是哪些即可.
解答 解:∵5-2=3,8-5=3,11-8=3,14-11=3,
∴2、5、8、11、14…这一列数是以2为首项,3为公差的等差数列;
∵$\frac{1}{2}+\frac{1}{5}+\frac{1}{20}+\frac{1}{14}+\frac{1}{35}+\frac{1}{41}+\frac{1}{1640}$+$\frac{1}{8}$=1,
∴这8个数可以是:2、5、8、14、20、35、41、1640.
点评 此题主要考查了规律型:数字的变化类问题,认真观察、仔细思考,善用联想是解决这类问题的方法,注意观察总结规律,并能正确的应用规律.

练习册系列答案
相关题目
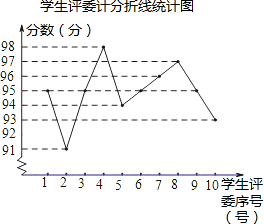
18.上学期,为创建文明城市,29中举行“社会主义核心价值观”演讲比赛,比赛聘请了10位老师和10位学生担任评委,其中九(7)班的得分情况如下面的统计图(表)所示:
老师评委计分统计表
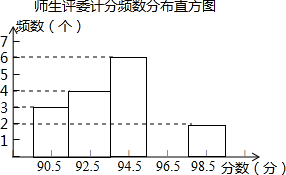
(1)在频数分布直方图中,自左向右第四组的频数为5.
(2)学生评委计分的中位数是95分.
(3)计算最后得分的规定如下:在评委的计分中各去掉一个最高分、一个最低分,分别计算平均数(老师、学生评委分开计算);并且按老师、学生评委的平均分各占60%、40%的方法计算各班最后得分,已知九(7)班最后得分为94.4分,求统计表中x的值.
老师评委计分统计表
| 评委序号/号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 计分/分 | 94 | 96 | 93 | 91 | x | 92 | 91 | 98 | 96 | 93 |


(1)在频数分布直方图中,自左向右第四组的频数为5.
(2)学生评委计分的中位数是95分.
(3)计算最后得分的规定如下:在评委的计分中各去掉一个最高分、一个最低分,分别计算平均数(老师、学生评委分开计算);并且按老师、学生评委的平均分各占60%、40%的方法计算各班最后得分,已知九(7)班最后得分为94.4分,求统计表中x的值.
3.小亮家新房屋装修,购进了同为50×50cm规格但品牌不同的两种瓷砖,他从这两种瓷砖(都是正方形)中各随机抽取五块测量,并将这十块瓷砖的边长(单位:cm)记录下表中:
算得两种品牌瓷砖边长的平均数相等,则从边长上可确定更标准的品牌为A.
| A种品牌 | 50.1 | 49.9 | 50.2 | 49.8 | 50.0 |
| B种品牌 | 50.3 | 49.6 | 50.0 | 50.4 | 49.7 |
20.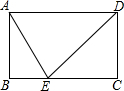 如图,点E是矩形ABCD边BC上一点,且cos∠DAE=$\frac{1}{2}$,tan∠ADE=1,若△ABE的面积是2$\sqrt{3}$,那么△ECD的面积是( )
如图,点E是矩形ABCD边BC上一点,且cos∠DAE=$\frac{1}{2}$,tan∠ADE=1,若△ABE的面积是2$\sqrt{3}$,那么△ECD的面积是( )
 如图,点E是矩形ABCD边BC上一点,且cos∠DAE=$\frac{1}{2}$,tan∠ADE=1,若△ABE的面积是2$\sqrt{3}$,那么△ECD的面积是( )
如图,点E是矩形ABCD边BC上一点,且cos∠DAE=$\frac{1}{2}$,tan∠ADE=1,若△ABE的面积是2$\sqrt{3}$,那么△ECD的面积是( )| A. | 2$\sqrt{3}$ | B. | 4$\sqrt{3}$ | C. | 6 | D. | 12 |
 如图是由若干块小立方体搭成几何体的主视图和俯视图,则这个几何体中小立方体的个数是9或10或11或12.
如图是由若干块小立方体搭成几何体的主视图和俯视图,则这个几何体中小立方体的个数是9或10或11或12. 如图,已知AB是⊙O的弦,CD是⊙O的直径,CD⊥AB,垂足为E,且点E是OD的中点,⊙O的切线BM与AO的延长线相交于点M,连接AC,CM.
如图,已知AB是⊙O的弦,CD是⊙O的直径,CD⊥AB,垂足为E,且点E是OD的中点,⊙O的切线BM与AO的延长线相交于点M,连接AC,CM.