题目内容
15.在同一平面内,有三条直线a、b、c,下列说法:①若a与b相交,b与c相交,则a与c相交;②若a∥b,b∥c,则a∥c;③若a⊥b,b⊥c,则a⊥c.其中正确命题是②.(填序号)分析 根据在同一平面内,垂直于同一条直线的两直线平行;如果两条直线都与第三条直线平行,那么这两条直线也互相平行进行分析即可.
解答 解:①若a与b相交,b与c相交,则a与c可能相交,也可能平行,故说法错误;
②若a∥b,b∥c,则a∥c,说法正确;
③若a⊥b,b⊥c,则a∥c,说法错误.
故答案为②.
点评 此题主要考查了平行公理和推论,关键是掌握同一平面内两直线的位置关系.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
3.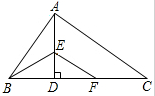 如用,Rt△ABC中,AB⊥AC,AD⊥BC,BE平分∠ABC,交AD于E,EF∥AC,下列结论中:①AB=BF;②AE=ED;③AD=DC;④∠ABE=∠DFE;⑤$\frac{AB}{BD}$=$\frac{CF}{DF}$,正确的是( )
如用,Rt△ABC中,AB⊥AC,AD⊥BC,BE平分∠ABC,交AD于E,EF∥AC,下列结论中:①AB=BF;②AE=ED;③AD=DC;④∠ABE=∠DFE;⑤$\frac{AB}{BD}$=$\frac{CF}{DF}$,正确的是( )
 如用,Rt△ABC中,AB⊥AC,AD⊥BC,BE平分∠ABC,交AD于E,EF∥AC,下列结论中:①AB=BF;②AE=ED;③AD=DC;④∠ABE=∠DFE;⑤$\frac{AB}{BD}$=$\frac{CF}{DF}$,正确的是( )
如用,Rt△ABC中,AB⊥AC,AD⊥BC,BE平分∠ABC,交AD于E,EF∥AC,下列结论中:①AB=BF;②AE=ED;③AD=DC;④∠ABE=∠DFE;⑤$\frac{AB}{BD}$=$\frac{CF}{DF}$,正确的是( )| A. | ①③ | B. | ①⑤ | C. | ③④ | D. | ①②⑤ |
4.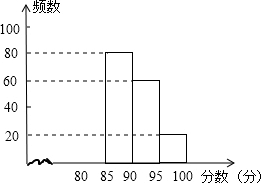 某校组织了“安全在我心中”知识竞赛活动.根据获奖同学在竞赛中的成绩制成的统计图表如下:
某校组织了“安全在我心中”知识竞赛活动.根据获奖同学在竞赛中的成绩制成的统计图表如下:
根据以上图表提供的信息,解答下列问题:
(1)求出表中a、b、c的数值,并补全频数分布直方图;
(2)如果成绩在95分以上(含95分)的可以获得特等奖,那么获奖的同学获得特等奖的概率是多少?
(3)获奖成绩的中位数落在哪个分数段?并估算全部获奖同学的平均分.
 某校组织了“安全在我心中”知识竞赛活动.根据获奖同学在竞赛中的成绩制成的统计图表如下:
某校组织了“安全在我心中”知识竞赛活动.根据获奖同学在竞赛中的成绩制成的统计图表如下:| 分数段 | 频数 | 频率 |
| 80≤x<85 | a | 0.2 |
| 85≤x<90 | 80 | b |
| 90≤x<95 | 60 | c |
| 95≤x<100 | 20 | 0.1 |
(1)求出表中a、b、c的数值,并补全频数分布直方图;
(2)如果成绩在95分以上(含95分)的可以获得特等奖,那么获奖的同学获得特等奖的概率是多少?
(3)获奖成绩的中位数落在哪个分数段?并估算全部获奖同学的平均分.
 如图所示,通过平移,△ABC的顶点A移到点D,画出平移后的图形,并找出图中所有平行且相等的线段.
如图所示,通过平移,△ABC的顶点A移到点D,画出平移后的图形,并找出图中所有平行且相等的线段.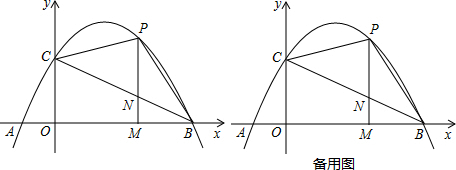
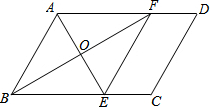 如图,在?ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,AE与BF相交于点O,连接EF.
如图,在?ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,AE与BF相交于点O,连接EF.