题目内容
15. 如图所示,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足$\frac{CF}{FD}$=$\frac{1}{3}$,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.给出下列结论:
如图所示,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足$\frac{CF}{FD}$=$\frac{1}{3}$,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.给出下列结论:①△ADF∽△AED;②FG=2;③DC平分∠ADE;④CG2=AG•BG;
其中结论正确的是( )
| A. | ①② | B. | ①②③ | C. | ①②④ | D. | ①②③④ |
分析 ①由AB是⊙O的直径,弦CD⊥AB,根据垂径定理可得:$\widehat{AD}$=$\widehat{CA}$,DG=CG,继而证得△ADF∽△AED;
②由$\frac{CF}{FD}$=$\frac{1}{3}$,CF=2,可求得DF的长,继而求得CG=DG=4,则可求得FG=2;
③可以结合DC平分∠ADE,进而得出结论与已知矛盾进而得出答案;
④利用圆周角定理以及相似三角形的判定与性质得出即可.
解答 解:①∵AB是⊙O的直径,弦CD⊥AB,
∴$\widehat{AD}$=$\widehat{AC}$,DG=CG,
∴∠ADF=∠AED,
∵∠FAD=∠DAE(公共角),
∴△ADF∽△AED;
故①正确;
②∵$\frac{CF}{FD}$=$\frac{1}{3}$,CF=2,
∴FD=6,
∴CD=DF+CF=8,
∴CG=DG=4,
∴FG=CG-CF=2;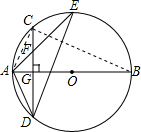
故②正确;
③连接AC,
∵由①得$\widehat{AD}$=$\widehat{AC}$,
∴当DC平分∠ADE时,$\widehat{AC}$=$\widehat{CE}$=$\widehat{AD}$,
∴∠CAE=∠ACD,
∴AF=FC,
又∵CF=2,AF=3,
∴FC≠AF,
∴③DC平分∠ADE错误;
④连接BC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠CAB+∠CBA=90°,
∴∠ACG=∠CBA,
又∵∠ACG=∠CGB,
∴△ACG∽△CBG,
∴$\frac{GC}{BG}$=$\frac{AG}{CG}$
∴CG2=AG•BG故此选项正确.
故选;C.
点评 此题考查了相似三角形的判定与性质、圆周角定理、垂径定理等知识,此题综合性较强,难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
11.某社区计划购买甲乙两种树苗共600棵,甲,乙两种树苗单价及成活率见下表:
(1)购买树苗资金刚好44000元,可购买甲乙树苗多少棵?
(2)若这批树苗的成活率为90%,则应购买甲、乙两种树苗各多少棵?
| 种类 | 单价 | 成活率 |
| 甲 | 60 | 88% |
| 乙 | 80 | 96% |
(2)若这批树苗的成活率为90%,则应购买甲、乙两种树苗各多少棵?
4.已知⊙O的半径为3,直线l到圆心O的距离为2,则直线l与⊙O的位置关系是( )
| A. | 相离 | B. | 相切 | C. | 相交 | D. | 不确定 |
5.6名学生中,初一、初二、初三各占2名,若从这6名学生中任意选取3名,实验估计选取的3名学生中,两两不在同一年段的概率,那么下列实物可以直接作为模拟实验中的替代物的是( )
| A. | 6个只有颜色不同的小球 | |
| B. | 两个骰子 | |
| C. | 三个硬币 | |
| D. | 只有颜色不同的小卡片6张,其中红、白、黄各占2张 |
 一辆摩托车从起点出发沿笔直的赛道向终点行驶,行驶中的速度V(km/h)与时间t(h)的关系部分信息如图所示,根据图象有下列说法:
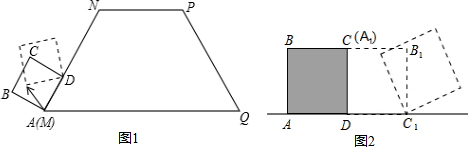
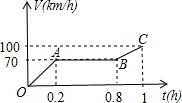
一辆摩托车从起点出发沿笔直的赛道向终点行驶,行驶中的速度V(km/h)与时间t(h)的关系部分信息如图所示,根据图象有下列说法: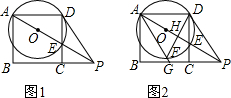 如图1,已知ABCD是边长为4的正方形,E是CD边上的一个动点,连接AE,AE的延长线交BC的延长线于点P,连接PD.作△ADE的外接圆⊙O.设DE=x,PC=y.
如图1,已知ABCD是边长为4的正方形,E是CD边上的一个动点,连接AE,AE的延长线交BC的延长线于点P,连接PD.作△ADE的外接圆⊙O.设DE=x,PC=y.