题目内容
16.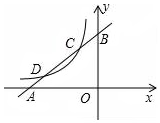 如图,已知直线y1=x+m与x轴、y轴分别交于A、B两点,与双曲线y2=$\frac{k}{x}$分别交于C、D两点,且点C的坐标为(-1,2).
如图,已知直线y1=x+m与x轴、y轴分别交于A、B两点,与双曲线y2=$\frac{k}{x}$分别交于C、D两点,且点C的坐标为(-1,2).(1)求直线AB及双曲线的解析式;
(2)求点D的坐标;
(3)利用函数图象直接写出:在第二象限内,当x在什么范围时,y1>y2?
分析 (1)根据y1=x+m与${y_2}=\frac{k}{x}$过点C(-1,2),代入得出m,k的值,即可得出直线AB及双曲线的解析式;
(2)把直线AB及双曲线的解析式联立列方程组,得点D的坐标;
(3)由函数图象可知:在第二象限内,当-2<x<-1时,y1>y2.
解答 解:(1)∵y1=x+m与${y_2}=\frac{k}{x}$过点C(-1,2),
∴m=2-(-1)=3,k=-1×2=-2;
∴直线AB及双曲线的解析式分别为y1=x+3,${y_2}=-\frac{2}{x}$;
(2)联立列方程组得$\left\{\begin{array}{l}y=x+3\\ y=-\frac{2}{x}\end{array}\right.$,
解得$\left\{\begin{array}{l}x=-1\\ y=2\end{array}\right.$或$\left\{\begin{array}{l}x=-2\\ y=1\end{array}\right.$,
∴点D的坐标为(-2,1);
(3)由函数图象可知:在第二象限内,当-2<x<-1时,y1>y2.
点评 本题考查了反比例函数和一次函数的交点问题,当有两个函数的时候,着重使用一次函数,体现了方程思想,综合性较强.

练习册系列答案
相关题目
7.当温度不变时,气球内气体的气压P(单位:kPa)是气体体积V(单位:m3)的函数,下表记录了一组实验数据:P与V的函数关系式可能是( )
| V(单位:m3) | 1 | 1.5 | 2 | 2.5 | 3 |
| P(单位:kPa) | 96 | 64 | 48 | 38.4 | 32 |
| A. | P=96V | B. | P=-16V+112 | C. | P=16V2-96V+176 | D. | P=$\frac{96}{V}$ |
4.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
1.-2017的绝对值是( )
| A. | $\frac{1}{2017}$ | B. | ±2017 | C. | 2017 | D. | -2017 |
6.关于x的二次函数y=-(x-1)2+2,下列说法中正确的是( )
| A. | 图象与y轴的交点坐标为(0,2) | B. | 当x>0时,y随x的增大而减小 | ||
| C. | 当x<0时,y随x的增大而增大 | D. | 当x>1时,y随x的增大而增大 |
 如图所示,有一块呈三角形的草坪,其一边长为20m,在这个草坪的图纸上,若这条边的长为5cm,其他两边的长都是3.5cm,则该草坪其他两边的实际长度为14m;14m.
如图所示,有一块呈三角形的草坪,其一边长为20m,在这个草坪的图纸上,若这条边的长为5cm,其他两边的长都是3.5cm,则该草坪其他两边的实际长度为14m;14m.