题目内容
如图，已知MN是线段AB的垂直平分线，垂足为O，点C、D在MN上，求证：∠CAD=∠CBD．考点：线段垂直平分线的性质
专题：证明题
分析：利用线段垂直平分线的性质可知CA=CB，DA=DB，加上CD=CD，可证明△ACD≌△BCD，可得到∠CAD=∠CBD．
解答：解：∵MN是线段AB的垂直平分线，且C、D在MN上，
∴CA=CB，DA=DB，
在△ACD和△BCD中，
，
∴△ACD≌△BCD（SSS），
∴∠CAD=∠CBD．
∴CA=CB，DA=DB，
在△ACD和△BCD中，
|
∴△ACD≌△BCD（SSS），
∴∠CAD=∠CBD．
点评：本题主要考查线段垂直平分线的性质，掌握线段垂直平分线上的点到线段两端点的距离相等是解题的关键．
练习册系列答案
相关题目
已知CD⊥AB于D，BE⊥AC于E 求证：D，B，C，E在同一圆上．如果x：y=2：3，则下列各式不成立的是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如图，圆内接四边形ABCD，两组对边的延长线分别相交于点E、F，且∠E=40°，∠F=60°，求∠A的度数．
如图是一个长方形的表面展开图，每个面上都标有一个数字，将它折叠复原成长方形，并使写有数字的面朝外．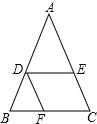
如图所示，已知DE∥BC，DF∥AC，且AE=3，AC=5，BC=10，求BF的长．若锐角A满足tana=
，则sina的值是（ ）
| 1 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|