题目内容
已知A(1,a),B(4,a)两点到直线的距离分别是
,
,则满足此条件的直线有几条 .
| 5 |
| 3 |
考点:坐标与图形性质
专题:数形结合
分析:根据A点和B点坐标得到AB=3,且AB∥x轴,再根据两点到直线的距离分别是
,
,则此直线与AB的交点在线段AB之间或线段AB的延长线,然后利用对称性可得到满足条件的直线有4条.
| 5 |
| 3 |
解答: 解:∵A(1,a),B(4,a),
解:∵A(1,a),B(4,a),
∴AB=3,且AB∥x轴,
而A(1,a),B(4,a)两点到直线l的距离分别是
,
,
∴l不可能平行坐标轴,
当l与直线AB的交点在线段AB之间时,利用对称性可得到满足条件l可作两条;
当l与直线AB的交点在线段AB的延长线时,利用对称性可得到满足条件l可作两条.
故答案为4.
 解:∵A(1,a),B(4,a),
解:∵A(1,a),B(4,a),∴AB=3,且AB∥x轴,
而A(1,a),B(4,a)两点到直线l的距离分别是
| 5 |
| 3 |
∴l不可能平行坐标轴,
当l与直线AB的交点在线段AB之间时,利用对称性可得到满足条件l可作两条;
当l与直线AB的交点在线段AB的延长线时,利用对称性可得到满足条件l可作两条.
故答案为4.
点评:本题考查了坐标与图形性质:利用点的坐标特征计算相应的线段长和判断线段与坐标轴的位置关系;记住各象限内点的坐标特征和坐标上点的坐标特征.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
已知抛物线y=-x2+bx+c的顶点坐标为(1,2),那么该抛物线有( )
| A、最大值2 | B、最小值2 |
| C、最大值1 | D、最小值1 |
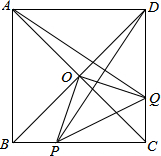 如图,O是正方形ABCD对角线的交点,Q是DC上任意一点,过点D作DE⊥AQ交BC于点P,求证:△OPQ是等腰直角三角形.
如图,O是正方形ABCD对角线的交点,Q是DC上任意一点,过点D作DE⊥AQ交BC于点P,求证:△OPQ是等腰直角三角形. 如图,△ABC的面积为
如图,△ABC的面积为 如图,∠ADB=
如图,∠ADB=