Question

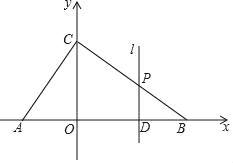
【题目】如图，在平面直角坐标系中，Rt△ABC的斜边AB在x轴上，点C在y轴上，∠ACB=90°，OC、OB的长分别是一元二次方程x2﹣6x+8=0的两个根，且OC＜OB．

（1）求点A的坐标；

（2）D是线段AB上的一个动点（点D不与点A，B重合），过点D的直线l与y轴平行，直线l交边AC或边BC于点P，设点D的横坐标为t，线段DP的长为d，求d关于t的函数解析式；

（3）在（2）的条件下，当d=时，请你直接写出点P的坐标．

Answer 1

【答案】（1）A（﹣1，0）；（2）d关于t的函数关系式为d=；

（3）当d=时，P点坐标为（﹣，）或（3，）．

【解析】

（1）由一元二次方程可求得OC、OB的长，利用△AOC～△COB可求得OA的长，则可求得A点.

（2）由A、B、C的坐标可分别求得直线AB、AC的解析式，当点D在线段OB上时，则点P在直线BC上，则可表示出P点坐标，从而可表示出PD的长；当点D在线段OA上时，则点P在直线AC上，可表示出点P的坐标，从而可表示出PD的长，即可求得d关于t的函数解析式.

（3）在（2）中所求的函数关系式中分别令d＝，分別求得相应的t的值，即可求得P点坐标．

（1）解方程x2﹣6x+8=0可得x=2或x=4，

∵OC、OB的长分别是一元二次方程x2﹣6x+8=0的两个根，且OC＜OB，

∴OC=2，OB=4，

∵∠ACB=90°，

∴∠ACO+∠BCO=∠ACO+∠CAO=90°，

∴∠CAO=∠BCO，且∠AOC=∠BOC，

∴△AOC∽△COB，

∴=，即=，解得AO=1，

∴A（﹣1，0）；

（2）由（1）可知C（0，2），B（4，0），A（﹣1，0），

设直线AC解析式为y=kx+b，

∴，解得，

∴直线AC解析式为y=2x+2，

同理可求得直线BC解析式为y=﹣x+2，

当点D在线段OA上时，即﹣1＜t≤0时，则点P在直线AC上，

∴P点坐标为（t，2t+2），

∴d=2t+2；

当点D在线段OB上时，即0＜t＜4时，则点P在直线BC上，

∴P点坐标为（t，﹣t+2），

∴d=﹣t+2；

综上可知d关于t的函数关系式为d=；

（3）在d=2t+2中，令d=，可得2t+2=，解得t=﹣，

∴P（﹣，）；

在d=﹣t+2中，令d=，可得﹣t+2=，解得t=3，

∴P（3，）；

综上可知当d=时，P点坐标为（﹣，）或（3，）．