题目内容
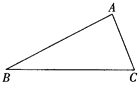
【题目】已知；如图，在△ABC中，AB＝BC，∠ABC＝90度．F为AB延长线上一点，点E在BC上，BE＝BF，连接AE、EF和CF．
（1）求证：AE＝CF；（2）若∠CAE＝30°，求∠EFC的度数．
【答案】（1）见解析；（2）∠EFC=30°．
【解析】
（1）根据已知利用SAS判定△ABE≌△CBF，由全等三角形的对应边相等就可得到AE=CF；（2）根据已知利用角之间的关系可求得∠EFC的度数．
（1）证明：在△ABE和△CBF中，
∵
，
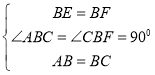∴△ABE≌△CBF（SAS）．
∴AE＝CF．
（2）解：∵AB＝BC，∠ABC＝90°，∠CAE＝30°，
∴∠CAB＝∠ACB＝
（180°﹣90°）＝45°，∠EAB＝45°﹣30°＝15°．
∵△ABE≌△CBF，
∴∠EAB＝∠FCB＝15°．
∵BE＝BF，∠EBF＝90°，
∴∠BFE＝∠FEB＝45°．
∴∠EFC＝180°﹣90°﹣15°﹣45°＝30°．
练习册系列答案
相关题目
【题目】天津市奥林匹克中心体育场—“水滴”位于天津市西南部的奥林匹克中心内，某校九年级学生由距“水滴”10千米的学校出发前往参观，一部分同学骑自行车先走，过了20分钟后，其余同学乘汽车出发，结果他们同时到达．已知汽车的速度是骑车同学速度的2倍，求骑车同学的速度．
（1）设骑车同学的速度为x千米/时，利用速度、时间、路程之间的关系填写下表．（要求：填上适当的代数式，完成表格）
速度（千米/时） | 所用时间（时） | 所走的路程（千米） | |
骑自行车 | x | 10 | |
乘汽车 | 10 |
（2）列出方程（组），并求出问题的解．
