题目内容
12.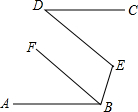 如图,AB∥CD,BF平分∠ABE,且BF∥DE,则∠ABE与∠D的关系是∠ABE=2∠D.
如图,AB∥CD,BF平分∠ABE,且BF∥DE,则∠ABE与∠D的关系是∠ABE=2∠D.
分析 延长BF与CD相交于M,根据两直线平行,同位角相等可得∠M=∠D,再根据两直线平行,内错角相等可得∠M=∠ABF,从而求出∠D=∠ABF,再根据角平分线的定义解答.
解答  解:延长BF与CD相交于M,
解:延长BF与CD相交于M,
∵BF∥DE,
∴∠M=∠D,
∵AB∥CD,
∴∠M=∠ABF,
∴∠D=∠ABF,
∵BF平分∠ABE,
∴∠ABE=2∠ABF,
∴∠ABE=2∠D.
故答案为:∠ABE=2∠D.
点评 本题考查了平行线的性质,角平分线的定义,作辅助线,是利用平行线的性质的关键,也是本题的难点.

练习册系列答案
相关题目
20.2100×(-$\frac{1}{2}$)99=( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
7. 如图,数轴上A、B两点分别对应实数a、b,则下列结论正确的是( )
如图,数轴上A、B两点分别对应实数a、b,则下列结论正确的是( )
 如图,数轴上A、B两点分别对应实数a、b,则下列结论正确的是( )
如图,数轴上A、B两点分别对应实数a、b,则下列结论正确的是( )| A. | a-b>0 | B. | ab>0 | C. | a+b>0 | D. | |a|-|b|>0 |
 B、C、D三点共线,且有正△ABC与正△CDE,F为AD的中点,G为BE中点,求证:CF=FG=CG.
B、C、D三点共线,且有正△ABC与正△CDE,F为AD的中点,G为BE中点,求证:CF=FG=CG.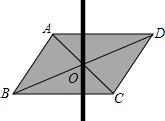 如图,用硬纸板剪一个平行四边形,作出它的对角线的交点O,用大头针把一根平放在平行四边形上的直细木条固定在点O处,并使细木条可以绕点O转动,拨动细木条,使它随意停留在任意位置,观察几次拨动的结果,你发现了什么?证明你的发现.
如图,用硬纸板剪一个平行四边形,作出它的对角线的交点O,用大头针把一根平放在平行四边形上的直细木条固定在点O处,并使细木条可以绕点O转动,拨动细木条,使它随意停留在任意位置,观察几次拨动的结果,你发现了什么?证明你的发现.