题目内容
2．
如图，在Rt△ABC中，∠C=90°，∠B=45°，a、b、c分别为∠A、∠B、∠C的对边，c=10，解这个直角三角形．
分析 先利用互余计算出∠A的度数，再利用∠A的正弦可计算出BC，于是可得到BC的长．
解答 解：∵∠C=90°，∠B=45°，
∴∠A=90°-45°=45°，
∴BC=AC，
∵sinA=$\frac{AC}{AB}$，
∴AC=10•sin45°=5$\sqrt{2}$，
∴BC=5$\sqrt{2}$．
点评 本题考查了解直角三角形：在直角三角形中，由已知元素求未知元素的过程就是解直角三角形．
练习册系列答案
津桥教育计算小状元系列答案
相关题目
12．定义：如果10b=n，那么称b为n的劳格数，记为b=d（n）．
（1）根据劳格数的定义，可知：d（10）=1，d（102）=2，那么：d（103）=3．
（2）劳格数有如下运算性质：若m、n为正数，则d（mn）=d（m）+d（n）；d（$\frac{m}{n}$）=d（m）-d（n）．
根据运算性质，填空：$\frac{{d（{2^5}）}}{d（2）}$=5，若d（3）=0.477，则d（9）=0.954，d（0.3）=-0.523．
（3）下表中与x数对应的劳格数d（x）有且只有两个是错误的，请找出错误的劳格数并改正．
（1）根据劳格数的定义，可知：d（10）=1，d（102）=2，那么：d（103）=3．
（2）劳格数有如下运算性质：若m、n为正数，则d（mn）=d（m）+d（n）；d（$\frac{m}{n}$）=d（m）-d（n）．
根据运算性质，填空：$\frac{{d（{2^5}）}}{d（2）}$=5，若d（3）=0.477，则d（9）=0.954，d（0.3）=-0.523．
（3）下表中与x数对应的劳格数d（x）有且只有两个是错误的，请找出错误的劳格数并改正．
| x | 1.5 | 3 | 5 | 6 | 8 | 9 | 12 | 27 |
| d（x） | 3a-b+c | 2a-b | a+c | 1+a-b-c | 3-3a-3c | 4a-2b | 3-b-2c | 6a-3b |
如图，△ABC的三个点分别是A（1，2），B（3，3），C（2，6）
如图，点M是AB的中点，点N是BD的中点，AB=$\frac{2}{3}$BC，且BC=12cm，CD=6cm．
在Rt△ABC中，∠C=90°，BC=$\sqrt{3}$，∠B的平分线BD=2$\sqrt{3}$，求∠DBC和∠ABD的度数．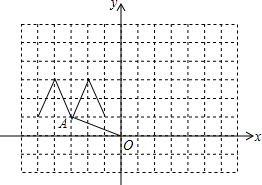
数学的英语单词为mathematical，画出第一个大写字母M绕着原点顺时针旋转90°，180°，270°后的图形，并计算出OA点所在运动的过程扫过的面积．
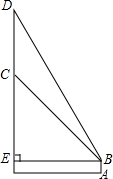如图，在一座楼房墙上有一面广告牌，小明站在楼房正面距离该楼房12米的A处，自B点看正前方的广告牌上端D处的仰角为60°，下端C处的仰角为45°．求该广告牌上下两端之间的距离CD．（结果精确到0.1米）