题目内容
18.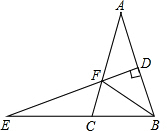 如图,△ABC中,AB=AC,AB的垂直平分线DE交BC的延长线于E,交AC于F,∠A=40°,AB+BC=6,则△BCF的周长为6,∠EFC的度数为50°.
如图,△ABC中,AB=AC,AB的垂直平分线DE交BC的延长线于E,交AC于F,∠A=40°,AB+BC=6,则△BCF的周长为6,∠EFC的度数为50°.
分析 由在△ABC中,AB=AC,∠A=40°,根据等腰三角形的性质,可求得∠ABC=∠ACB=70°,又由AB的垂直平分线DE交BC的延长线于E,交AC于F,可求得∠F的度数,继而求得∠EFC的度数,易得△BCF的周长=BC+AC=BC+AB.
解答 解:∵在△ABC中,AB=AC,∠A=40°,
∴∠ABC=∠ACB=70°,
∵DE是AB的垂直平分线,
∴AF=BF,∠BDE=90°,
∴∠E=90°-∠ABC=20°,
∴∠EFC=∠ACB-∠E=50°;
∵AB+BC=6,
∴△BCF的周长为:BC+CF+BF=BC+CF+AF=BC+AC=BC+AB=6.
故答案为:6,50°.
点评 此题考查了线段垂直平分线的性质以及等腰三角形的性质.注意垂直平分线上任意一点,到线段两端点的距离相等.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
 如图,已知点D,E分别在AC、AB上,∠B=∠C.除对顶角外.图中还有哪些角分别相等?证明你的结论.
如图,已知点D,E分别在AC、AB上,∠B=∠C.除对顶角外.图中还有哪些角分别相等?证明你的结论. 如图,在△ABC中,BC=12,∠BAC=100°,AB的垂直平分线交BC边于点E,AC的垂直平分线交BC边于点G,求∠EAG的度数和△AEG的周长.
如图,在△ABC中,BC=12,∠BAC=100°,AB的垂直平分线交BC边于点E,AC的垂直平分线交BC边于点G,求∠EAG的度数和△AEG的周长.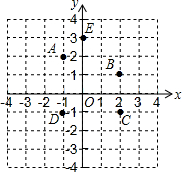 写出如图中的点A、B、C、D、E、F的坐标,观察这些点的坐标,回答下列问题.
写出如图中的点A、B、C、D、E、F的坐标,观察这些点的坐标,回答下列问题.