题目内容
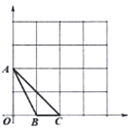
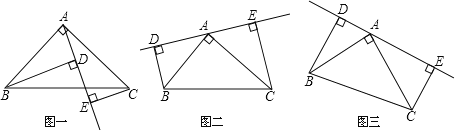
【题目】 如图①,在![]() 中
中![]() ,
,![]() ,
,![]() 是过
是过![]() 的一条直线,且
的一条直线,且![]() ,
,![]() 在
在![]() 的异侧,
的异侧,![]() 于
于![]() ,
,![]() 于
于![]() .
.
(1)填空:线段![]() 与
与![]() 、
、![]() 之间的数量关系为________;
之间的数量关系为________;
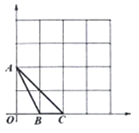
(2)若直线![]() 绕
绕![]() 点旋转到如图②位置时(
点旋转到如图②位置时(![]() ),其他条件不变,判断
),其他条件不变,判断![]() 与
与![]() ,
,![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
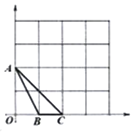
(3)若直线![]() 绕
绕![]() 点旋转到如图③位置时(
点旋转到如图③位置时(![]() ),其他条件不变,则
),其他条件不变,则![]() 与
与![]() ,
,![]() 的关系又怎样?请写出结果,不必证明.
的关系又怎样?请写出结果,不必证明.
【答案】(1)![]() ;(2)
;(2)![]() ,理由详见解析;(3)
,理由详见解析;(3)![]()
【解析】
(1)根据已知条件证△ABD与△CAE全等,得到![]() ,
,![]() ,由AE=AD+DE即可证得
,由AE=AD+DE即可证得![]() ;(2)先证明△ABD与△CAE全等,得到
;(2)先证明△ABD与△CAE全等,得到![]() ,
,![]() ,由DE=AD+AE得到
,由DE=AD+AE得到![]() ;(3)先证明△ABD与△CAE全等,得到
;(3)先证明△ABD与△CAE全等,得到![]() ,
,![]() ,由DE=AD+AE得到
,由DE=AD+AE得到![]()
(1)![]()
解:(2)![]() .理由如下:
.理由如下:
∵ ![]() ,
,
∴ ![]() ,
,
∵ ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
又∵ ![]() ,
,![]()
∴ ![]() .
.
在![]() 和
和![]() 中,
中,
∵  ,
,
∴ ![]() ,
,
∴ ![]() ,
,![]() ,
,
∵ ![]() ,
,
∴ ![]() .
.
(3)![]() ;
;
理由:∵ ![]() ,
,
∴ ![]() ,
,
∵ ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
又∵ ![]() ,
,![]()
∴ ![]() .
.
在![]() 和
和![]() 中,
中,
∵  ,
,
∴ ![]() ,
,
∴ ![]() ,
,![]() ,
,
∵ ![]() ,
,
∴ ![]() .
.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目