题目内容
工程营接到一项铺设管道任务,若每小时铺30米,那么比规定时间早50分钟完成,若每小时铺25米,那么比规定时间晚36分钟完成,现在工程队根据自身状况,打算比规定时间早3小时完成,问,每小时应疏通管道多少米?
考点:一元一次方程的应用
专题:应用题
分析:先设规定时间为x小时,利用工程总量相等得到30(x-
)=25(x+
),解得x=8,再设打算比规定时间早3小时完成,每小时应疏通管道y米,然后利用
工程总量相等得到y•(8-3)=30•(8-
),然后解一元一次方程即可.
| 50 |
| 60 |
| 36 |
| 60 |
工程总量相等得到y•(8-3)=30•(8-
| 50 |
| 60 |
解答:解:设规定时间为x小时,
根据题意得30(x-
)=25(x+
),
解得x=8,
设打算比规定时间早3小时完成,每小时应疏通管道y米,
根据题意得y•(8-3)=30•(8-
),
解得y=43.
答:每小时应疏通管道43米.
根据题意得30(x-
| 50 |
| 60 |
| 36 |
| 60 |
解得x=8,
设打算比规定时间早3小时完成,每小时应疏通管道y米,
根据题意得y•(8-3)=30•(8-
| 50 |
| 60 |
解得y=43.
答:每小时应疏通管道43米.
点评:本题考查了一元一次方程的应用:首先审题找出题中的未知量和所有的已知量,直接设要求的未知量或间接设一关键的未知量为x,然后用含x的式子表示相关的量,找出之间的相等关系列方程、求解、作答,即设、列、解、答.

练习册系列答案
相关题目
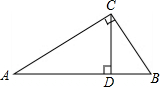 如图,∠ACB=90°,CD⊥AB,求证:△ACD∽△CBD∽ABC.
如图,∠ACB=90°,CD⊥AB,求证:△ACD∽△CBD∽ABC. 画出△ABC绕边AB的中点O旋转180°后的图形.
画出△ABC绕边AB的中点O旋转180°后的图形.