题目内容
已知关于x的一元二次方程(m-1)x2-(2m+1)x+m=0,当m取何值时:
(1)方程有两个不相等的实数根;
(2)方程有两个相等的实数根,并求出根;
(3)方程没有实数根.
(1)方程有两个不相等的实数根;
(2)方程有两个相等的实数根,并求出根;
(3)方程没有实数根.
考点:根的判别式
专题:
分析:(1)根据关于x的一元二次方程(m-1)x2-(2m+1)x+m=0有两个不相等的实数根时,△>0,列式求解即可.
(2)根据关于x的一元二次方程(m-1)x2-(2m+1)x+m=0有两个不相等的实数根时,△=0,求出m的值,再代入计算即可,
(3)根据关于x的一元二次方程(m-1)x2-(2m+1)x+m=0有两个不相等的实数根时,△<0,列式求解即可.
(2)根据关于x的一元二次方程(m-1)x2-(2m+1)x+m=0有两个不相等的实数根时,△=0,求出m的值,再代入计算即可,
(3)根据关于x的一元二次方程(m-1)x2-(2m+1)x+m=0有两个不相等的实数根时,△<0,列式求解即可.
解答:解:(1)∵关于x的一元二次方程(m-1)x2-(2m+1)x+m=0有两个不相等的实数根,
∴△=[-(2m+1)]2-4(m-1)m>0,且m-1≠0
∴m>-
且m≠1;
(2)∵关于x的一元二次方程(m-1)x2-(2m+1)x+m=0有两个相等的实数根,
∴△=[-(2m+1)]2-4(m-1)m=0,
∴m=-
,
原方程可变形为:-
x2-6x-1=0,
解得;x=-
;
(3)∵关于x的一元二次方程(m-1)x2-(2m+1)x+m=0没有实数根,
∴△=[-(2m+1)]2-4(m-1)m<0,
∴m<-
,
∴△=[-(2m+1)]2-4(m-1)m>0,且m-1≠0
∴m>-
| 1 |
| 8 |
(2)∵关于x的一元二次方程(m-1)x2-(2m+1)x+m=0有两个相等的实数根,
∴△=[-(2m+1)]2-4(m-1)m=0,
∴m=-
| 1 |
| 8 |
原方程可变形为:-
| 9 |
| 8 |
解得;x=-
| 1 |
| 3 |
(3)∵关于x的一元二次方程(m-1)x2-(2m+1)x+m=0没有实数根,
∴△=[-(2m+1)]2-4(m-1)m<0,
∴m<-
| 1 |
| 8 |
点评:此题考查了一元二次方程根的判别式,当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根,也考查了解一元二次方程.

练习册系列答案
相关题目
满足(x-3)2+(y-3)2=6的所有实数对(x,y),使
取最大值,此最大值为( )
| y |
| x |
A、3+2
| ||
B、4+
| ||
C、5+3
| ||
D、5+
|
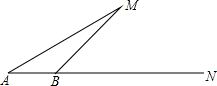 有一次,小明坐着轮船由A点出发沿正东方向AN航行,在A点望湖中小岛M,测得∠MAN=30°,航行100米到达B点时,测得∠MBN=45°,你能算出A点与湖中小岛M的距离吗?
有一次,小明坐着轮船由A点出发沿正东方向AN航行,在A点望湖中小岛M,测得∠MAN=30°,航行100米到达B点时,测得∠MBN=45°,你能算出A点与湖中小岛M的距离吗? 已知一次函数y=kx+b的图象与反比例函数
已知一次函数y=kx+b的图象与反比例函数 已知:AB∥EF,BC∥DE,AD=FC,求证:AB=EF.
已知:AB∥EF,BC∥DE,AD=FC,求证:AB=EF. 如图,已知:E、F分别是AB和CD上的点,DE、AF分别交BC于G、H,∠1=∠2,∠A=∠D,求证:
如图,已知:E、F分别是AB和CD上的点,DE、AF分别交BC于G、H,∠1=∠2,∠A=∠D,求证: 如图,∠E=∠F,∠A=∠C,试说明AB∥DC.
如图,∠E=∠F,∠A=∠C,试说明AB∥DC.