题目内容
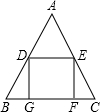 如图,在△ABC中,AB=AC,点D、E分别是边AB、AC的中点,点G、F在BC边上,四边形DEFG是正方形.若DE=2cm,则AB的长为
如图,在△ABC中,AB=AC,点D、E分别是边AB、AC的中点,点G、F在BC边上,四边形DEFG是正方形.若DE=2cm,则AB的长为考点:三角形中位线定理,勾股定理,正方形的性质
专题:
分析:根据三角形的中位线平行于第三边并且等于第三边的一半可得BC=2DE,过点A作AH⊥BC与H,然后求出AH等于正方形的边长的2倍,再根据等腰三角形三线合一的性质可得BH=
BC,然后利用勾股定理列式计算即可得解.
| 1 |
| 2 |
解答: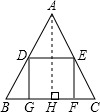 解:∵点D、E分别是边AB、AC的中点,
解:∵点D、E分别是边AB、AC的中点,
∴DE是△ABC的中位线,
∴BC=2DE=2×2=4cm,
过点A作AH⊥BC与H,
则AH=2EF=2DE=2×2=4cm,
BH=
BC=
×4=2cm,
在Rt△ABH中,由勾股定理得,AB=
=
=2
cm.
故答案为:2
cm.
 解:∵点D、E分别是边AB、AC的中点,
解:∵点D、E分别是边AB、AC的中点,∴DE是△ABC的中位线,
∴BC=2DE=2×2=4cm,
过点A作AH⊥BC与H,
则AH=2EF=2DE=2×2=4cm,
BH=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△ABH中,由勾股定理得,AB=
| AH2+BH2 |
| 42+22 |
| 5 |
故答案为:2
| 5 |
点评:本题考查了三角形的中位线平行于第三边并且等于第三边的一半,正方形的性质,等腰三角形三线合一的性质,勾股定理,熟记性质与定理并作辅助线构造出直角三角形是解题的关键.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
若不等式组
有解,则a的取值范围是( )
|
| A、a>1 | B、a≥1 |
| C、a≤-1 | D、a<-1 |
 如图,点A、B、C均在⊙O上,∠C=50°,则∠OAB=
如图,点A、B、C均在⊙O上,∠C=50°,则∠OAB= 如图,在四边形ABCD中,对角线AC,BD交于点O,OA=OC,OB=OD,添加一个条件使四边形ABCD是菱形,那么所添加的条件可以是
如图,在四边形ABCD中,对角线AC,BD交于点O,OA=OC,OB=OD,添加一个条件使四边形ABCD是菱形,那么所添加的条件可以是 如图,直线y=kx+b交坐标轴于A、B两点,则不等式kx+b>0的解集是
如图,直线y=kx+b交坐标轴于A、B两点,则不等式kx+b>0的解集是