题目内容
若不等式组
有解,则a的取值范围是( )
|
| A、a>1 | B、a≥1 |
| C、a≤-1 | D、a<-1 |
考点:解一元一次不等式组
专题:计算题
分析:先解出不等式组的解集,根据已知不等式组
有解,求a的取值范围.
|
解答:解:
,
解①得x≥-a,
解②得x<-1,
∴不等式组的解集为:-a≤x<-1.
∵不等式组有解,
∴-a<-1,即a>1,
∴a的取值范围是a>1,
故选:A.
|
解①得x≥-a,
解②得x<-1,
∴不等式组的解集为:-a≤x<-1.
∵不等式组有解,
∴-a<-1,即a>1,
∴a的取值范围是a>1,
故选:A.
点评:本题考查了解一元一次不等式组:分别求出不等式组各不等式的解集,然后根据“同大取大,同小取小,大于小的小于大的取中间,大于大的小于小的无解”确定不等式组的解集.

练习册系列答案
相关题目
 如图,把矩形ABCD沿EF折叠,点A、B分别落在A′、B′处.A′B′与AD交于点G,若∠CFB′=60°,则∠AEF=( )
如图,把矩形ABCD沿EF折叠,点A、B分别落在A′、B′处.A′B′与AD交于点G,若∠CFB′=60°,则∠AEF=( )| A、110° | B、115° |
| C、120° | D、130° |
 如图,□CEFH的边长为m,点D在射线CH上移动,以CD为边作□CDAB,连接AE、AH、HE,在D点移动的过程中,△AHE的面积( )
如图,□CEFH的边长为m,点D在射线CH上移动,以CD为边作□CDAB,连接AE、AH、HE,在D点移动的过程中,△AHE的面积( )| A、无法确定 | ||
B、
| ||
C、
| ||
D、
|
2014年广州市共有约11.2万考生参加广州中考,请用科学记数法表示这个数( )
| A、11.2×104 |
| B、1.12×104 |
| C、1.2×104 |
| D、1.12×105 |
预计全国参加高等院校统一招生考试的学生约10 153 000人,其中10 153 000用科学记数法表示应为( )
| A、10.153×106 |
| B、1.0153×107 |
| C、0.10153×108 |
| D、1.0153×109 |
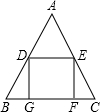 如图,在△ABC中,AB=AC,点D、E分别是边AB、AC的中点,点G、F在BC边上,四边形DEFG是正方形.若DE=2cm,则AB的长为
如图,在△ABC中,AB=AC,点D、E分别是边AB、AC的中点,点G、F在BC边上,四边形DEFG是正方形.若DE=2cm,则AB的长为 为了了解九年级学生的体育成绩,某校进行完体育测试后,对这次体育测试成绩进行了抽样调查,结果统计如下,其中扇形统计图中C组所在扇形的圆心角度数为36°.
为了了解九年级学生的体育成绩,某校进行完体育测试后,对这次体育测试成绩进行了抽样调查,结果统计如下,其中扇形统计图中C组所在扇形的圆心角度数为36°.